Modul 2.1: Lineær algebra for 3D grafikk

Dette er en kort introduksjon til matematikken som brukes i sammenheng med 3D datamaskingrafikk. 

Nøkkelord: Lineær algebra, vektorer, matriser, transformasjoner, matrisemultiplikasjon, normalvektor, normalisering, invers matrise, transponert matrise.

Vektorer 

Vektorer har en avgjørende rolle i forbindelse med bl.a. grafikk, animasjoner, kollisjonsdeteksjon og ulike fysiske simuleringer. En vektor har både en retning (direction) og en størrelse (magnitude).

Enheter som i sin natur består av både retning og størrelse kaller vi gjerne en vektorstørrelse (vector valued quantities). Eksempler er kraft (har en retning og ”styrke”), forskyvning (retning og avstand), fart (retning og hastighet). 

Vi kan også bruke vektorer til å beskrive kun retning – for eksempel hvilken retning vi ser inn i en spillverden, hvilken retning en polygon har, fra hvilken retning lyset kommer m.m.

Vektorer tegnes gjerne som piler med en retning og en lengde som vist i figuren under.

I prinsippet er to vektorer med samme retning og lengde lik - i figuren er og lik siden de har samme retning og lengde. Plassering av vektorene er (i prinsippet) ikke viktig – vi kan godt flytte på og fortsatt si at .

For at vi skal kunne jobbe med vektorer må vi imidlertid kunne kvantifisere vektorstørrelsene (størrelse og retning). Vi plasserer dem derfor inn i et 3D koordinatsystem slik at ”halen” til vektorene starter i origo (standardposisjon). 

Vi kan nå angi enhver vektor ved å spesifisere koordinatene til ”vektorhodet”, slik: . Dette betyr at vi kan spesifisere en vektor vha. 3 flyttall i datamaskinen.

To vektorer som har samme lengde og retning kan ”plasseres” i to ulike koordinatsystemer og fortsatt være like. Dette er analogt med for eksempel temperatur – vann har samme kokepunkt enten vi spesifiserer dette i Celcius (100) eller Fahrenheit (212).

På samme måte kan vi bruke ulike måleskalaer for å måle vind (m/s, km/t). Vinden blåser i en bestemt retning med en bestemt hastighet. Vi kan måle dette i forhold til ulike referanserammer (eller koordinatsystemer) men vinden har uansett samme retning og hastighet.

Dette er viktig og betyr at når vi kvantifiserer en vektor (vha. koordinatverdier) er disse i forhold til en referanseramme (et koordinatsystem). I vår sammenheng (grafikk) er det ofte behov for å utnytte ulike referanserammer (koordinatsystemer). Det er derfor viktig å holde rede på hvilken referanseramme/koordinatsystem en vektor er definert i. I tillegg må vi vite hvordan vi kan konvertere vektorer mellom de ulike koordinatsystemene.

Legg merke til at både vektorer og punkter kan beskrives vha. koordinatene (x,y,z) i forhold til et koordinatsystem. Matematisk er de allikevel ikke det samme – et punkt representerer en lokasjon i rommet mens en vektor representerer en størrelse og en retning.

Venstrehånds- og høyrehånds koordinatsystemer

WebGL bruker et såkalt høyrehånds koordinatsystem. Dersom du vender innsiden av høyre hånd opp, strekker tommelen rett ut og vender resten av fingrene opp (90 grader i forhold til håndflaten) vil tommelen peke i positiv Z-retning, resten av fingrene peke i positiv Y-retning mens hele hånden peker i positiv X-retning (se figur under). Tilsvarende for venstrehåndssystem.

Dette betyr at når vi definerer 3D modeller i WebGL angir vi punktene i forhold til et høyrehåndssystem. OpenGL bruker også høyrehåndssystemet mens Direct3D bruker venstrehåndssystemet.

Grunnleggende vektoroperasjoner

To vektorer er like dersom tilsvarende komponenter er like:

La og være to vektorer:

og er like dersom vx = ux, vy = uy og vz = uz

Vi legger sammen to vektorer slik:

La og være to vektorer. En vektoraddisjon er definert slik:

+ = (ux + vx, uy + vy , uz + vz).

Vi multipliserer en vektor med en skalarverdi slik:

La k være en skalarverdi og : k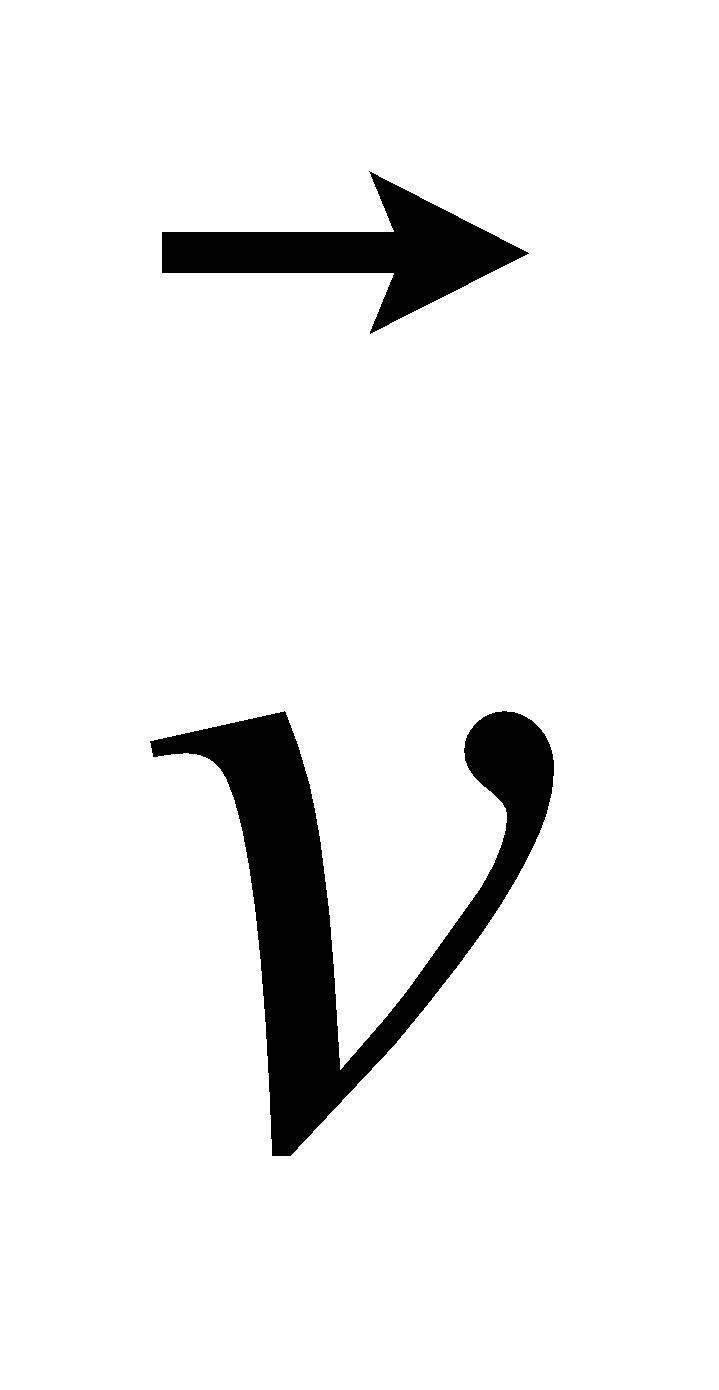= (k vx, k vy, k vz).

Vi kan definere vektorsubtraksjon vha. vektoraddisjon.

Vi kan enkelt utføre grunnleggende vektoroperasjoner i Matlab eller Octave (http://www.gnu.org/software/octave/). Under ser du et eksempel på dette. I kommandovinduet til Matlab legger man inn vektorer (i form av Matlab-variabler) samt utfører aktuell operasjon. Eksemplet under viser addisjon av to vektorer.

Vi starter med å angi to vektorer:

>>u=[1 2];
>>v=[2 0.5];
>>u+v
ans = 3.0 2.5

Vi oppgir med andre ord vektorer vha. klammeparenteser og skiller verdiene med et mellomrom. Når vi skriver u+v og trykker enter beregnes svaret.

Lengde og normalisering

Lengden til en vektor beregnes slik (Pytagoras):

I enkelte sammenhenger er vi ikke interessert i lengden men ønsker at vektoren skal ha lengden 1. Dette kalles normalisering. Vi normaliserer en vektor slik:

Dette betyr at x,y og z-verdiene vil få verdier mellom 0 og 1 mens lengden på vektoren blir lik 1.

Prikkprodukt

Prikkproduktet (kalles også indreprodukt eller skalarprodukt) mellom to vektorer er en form for vektormultiplikasjon som resulterer i en skalarverdi. La og være to vektorer. Prikkproduktet mellom disse er da:

Prikkproduktet er altså summen av produktene av enkeltkomponentene.

Dette har tilsynelatende liten mening – snur vi imidlertid litt på ting får vi at:

Dette kan dermed brukes til å finne vinkelen mellom to vektorer:

Matlab:

Her kan vi angi vektorene slik:

>>u=[-4 0 -1];

>>v=[1 2 3];

>>dot(u,v)

ans = -7

Her oppgir vi først to vektorer (med navn u og v). Deretter beregnes prikkproduktet som gir en skalarverdi som svar (-7).

Videre finner vi vinkelen mellom disse slik:

>> ul=sqrt(u(1,1)*u(1,1) + u(1,2)*u(1,2) + u(1,3)*u(1,3));

>> vl=sqrt(v(1,1)*v(1,1) + v(1,2)*v(1,2) + v(1,3)*v(1,3));

>> dp=dot(u,v);

>> cosFi= dp /(ul*vl);

>> acosd(cosFi)

ans = 116.9841

Kryssproduktet

Kryssproduktet mellom to vektorer evaluerer til en ny vektor. Kryssproduktet mellom to 3D- vektorer gir en ny vektor som er gjensidig ortogonal til de to opprinnelige vektorene. Dette betyr at den nye vektoren står vinkelrett på flaten definert av de to opprinnelige vektorene.

Kryssproduktet er definert slik:

Dersom du med din høyre hånd peker pekefingeren i retning av den første vektoren,, og ringfingeren i retning av den andre vektoren, , vil tommelen peke i sin retning. Dette kalles høyrehåndsregelen for kryssprodukt.

Kryssproduktet er ikke-kommutativt, dvs. er ikke det samme som . Det kan imidlertid vises at

Kryssproduktet kan for eksempel brukes til å finne normalvektorer som er aktuell i forbindelse med lysberegning i WebGL.

Matlab:

Vi starter med å angi to vektorer:

>>u=[2 1 3];

>>v=[2 0 0];

>>w=cross(u,v)

w = 0 6 -2

>> y=cross(v,u)

y = 0 -6 2

Her beregnes kryssproduktet mellom u og v samt v og u. Vi ser at .

Punkter

Vi kan også bruke en vektor til å spesifisere en 3D-lokasjon i rommet – vi kaller dette en posisjonsvektor eller bare punkt. I dette tilfellet er det lokasjonen til ”vektorhodet” som er av interesse – ikke lengden eller retninga.

Vektorer, Javascript & WebGL

Det finnes flere gode Javascript-biblioteker som inneholder vektor-klasser som vi kan bruke.

Noen eksempler:

• Sylvester (Sylvester, 2012)
• WebGL-mjs (WebGL-mjs, 2010)
• glMatrix (glMatrix)
• cuon-matrix.js (Matsuda, K. et al, 2013)

I følgende eksempler broker vi Sylvester-bibilioteket fra Javascript-koden.

Vektorsum

Anta at vi skal summere vektorene 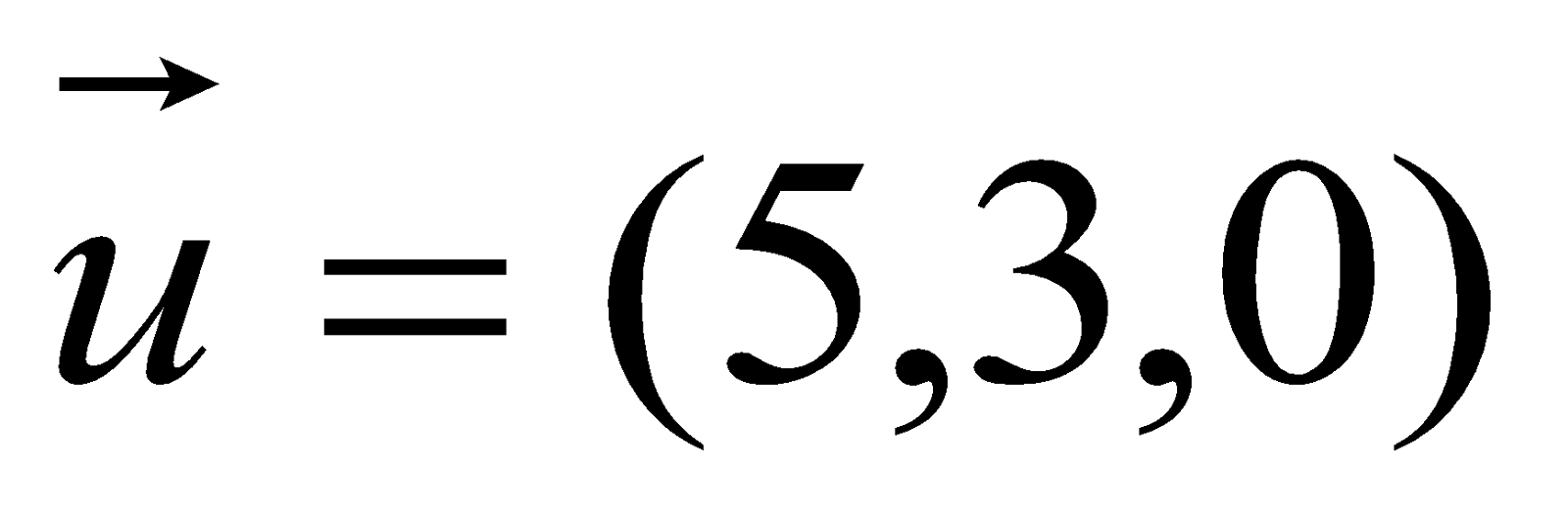og .

let u = Vector.create([5.0, 3.0, 0.0]);

let v = Vector.create([4.0, -2.0 , 0.0]);

let sumV = u.add(v);

Dette vil gi vsum=(9,1,0).

Vektorsubtraksjon

let u = Vector.create([5.0, 3.0, 0.0]);

let v = Vector.create([4.0, -2.0 , 0.0]);

let vdif = u.subtract(v);

Dette vil gi vdif=(1,5,0).

Skalering av vektorer

Skalering av en vektor betyr at vi multipliserer vektoren med en skalarverdi.

let a = Vector.create([9.0, 1.0, 0.0]);

let fscale = 2.0;

let vprod = a.multiply(fscale);

Dette vil gi vprod=(18,2,0).

Multipliserer man vektoren med et tall mindre enn 1 nedskalerer man vektoren.

Finne normalen mellom to vektorer

En normalvektor er en vektor som står vinkelrett (ortogonal) på en flate. En normal representerer en retning noe som betyr at posisjonen ikke er viktig. I forbindelse med grafikk er det ofte aktuelt å beregne normalvektorer i forbindelse med lysberegning. 

Man kan for eksempel finne normalen til en flate representert av to vektorer som har samme ”startpunkt”. Se figuren under.

Vi kan bruke kryssproduktet til å beregne normalvektoren til en flate definert av vektorene v1 og v2. Eksempel:

let v1 = Vector.create([0.0, 2.0, 0.0]);   

let v2 = Vector.create([3.0, 1.0 , 0.0]);

let w = v1.cross(v2);  //= v1 x v2

Dette betyr at man multipliserer vektorene slik: w = v1 x v2 som gir vektoren [0,0,-6] som resultat.

Dette stemmer også med høyrehåndsregelen for kryssprodukt (se punkt over om kryssprodukt). Det motsatte, dvs: w = v2.cross(v1) gir w = [0,0,6], altså en vektor som peker i motsatt retning.

Normalisering av en vektor

Ofte er det behov for å skalere vektorer til enhetsvektorer. Dette betyr at vektorverdiene (x,y og z) skaleres til verdier mellom 0 og 1 men der forholdet mellom dem fortsatt er det samme som i den opprinnelige vektoren. Lengden på vektoren blir lik 1. Dette gjøres ved å dividere enkeltkomponentene i vektoren med lengden på vektoren (se tidligere beskrivelse). I Javascript (med Sylvester-biblioteket, se over) kan man gjøre følgende:

let v3 = Vector.create([5.0, 2.0 , 1.0]);

let v3unit = v3.toUnitVector();

let length = v3unit.distanceFrom([0,0,0]);

Legg merke til hvordan lengden på vektoren kan beregnes vha. distanceFrom() metoden. Her beregenes lengden fra [0,0,0] for å sjekke at vektoren faktiska har lengde = 1.

Finne vinkelen mellom to vektorer – prikkprodukt

Vi kan bruke prikkproduktet til å finne vinkelen mellom to vektorer. Prikkproduktet kan for eksempel brukes til å beregne kulebaner, refleksjonsvinkler eller lysintensitet. Formelen for prikkproduktet ble vist i et tidligere kapittel. Javscript (m/Sylvester):

let u1 = Vector.create([0.0, 5.0, 0.0]);

let v1 = Vector.create([5.0, 5.0, 0.0]);

   

let dp1 = u1.dot(v1); //= 32?

let u1L = u1.distanceFrom([0,0,0,]);    //Lengden til u1

let v1L = v1.distanceFrom([0,0,0,]);    //Lengden til v1

let cosFi = dp1 / (u1L * v1L);          //Vinkelen mellom dem!

let angle = toDegrees(Math.acos(cosFi));

. . .

function toDegrees (angle) {

 return angle * (180 / Math.PI);

}

Dette vil gi angle lik 45 grader som er vinkelen mellom vektor u1 og v1.

Matriser og transformasjoner

Innenfor området 3D datamaskingrafikk er matrisen en fundamental komponent. Matriser brukes til ulike transformasjoner som å flytte (translere), rotere eller skalere 3D modeller samt til å simulere kamera og gjøre ulike projeksjoner.

Dersom man skal få et bedre ”grep” om, samt utnytte mulighetene i forbindelse med «3D-programmering», er det er viktig å forstå grunnleggende matrisematematikk.

De nevnte Javascript-bibliotekene (Sylvester m.fl., se over) har mange ferdige klasser og funksjoner som vi kan bruke til dette.

Essensen er at vi bruker matriser til å transformere posisjonsvektorer (punkter). Multipliserer vi en posisjonsvektor med en matrise får vi en ny og transformert posisjonsvektor. 3D modeller beskrives vha. et sett punkter (vertekser) i 3D rommet. Dersom vi transformerer alle punktene til modellen vha. samme matrise har vi transformert hele modellen.

En matrise er en samling med (flyt)tall organisert i rader og kolonner. Produktet av antall rader og kolonner gir matrisas dimensjon. Tallene i matrisa kalles elementer. Vi angir elementene i matrisa vha. en indeks, slik; Mij der i angir rad og j kolonne for element M.

Man indekserer for eksempel elementene i en (4x4) matrise som vist under:

Under er det vist noen eksempler på matriser:

             

Matrise A er en 4x4 matrise, B en 3x2, u en 1x4 og v en 3x1 matrise. Her er u og v spesielle matriser som består av henholdsvis en rad og en kolonne. Disse kalles gjerne rad og kolonnevektorer siden de kan brukes til å representere vektorer på matriseform (vi kan derfor velge om vi ønsker å bruke notasjonen (x,y,z) eller [x, y, z]).

Matriser kan enten være basert på radvektorer eller kolonnevektorer. I en radvektor-basert matrise kan vi se på hver rad som en vektor mens i en kolonnevektorbasert matrise er hver kolonne en vektor.

To matriser er like dersom alle elementene i begge matriser er like. Vi adderer matriser (av samme dimensjon) ved å addere enkeltelementene. Vi multipliserer en matrise med en skalarverdi ved å multiplisere hver enkelt element med skalarverdien. Subtraksjon uttrykkes vha. addisjon, slik: A – B = A + (-1*B) = A + (-B).

Matrisemultiplikasjon

I dette avsnittet skal vi se på hvordan man kan multiplisere matriser med hverandre og vektorer med matriser.

Matrise * matrise

Dette brukes for eksempel i de tilfeller der man skal utføre sammensatte transformasjoner som for eksempel en translasjon (forflytning) etterfulgt av en rotasjon.

Dersom A en en m*n matrise og B er en n*p matrise er produktet AB definert og gir en m*p matrise, C. I C er mij lik prikkproduktet av radvektor i i A og kolonnevektor j i B, dvs.

       

Eksempel:

Produktet AB er nå definert som en 2*3 matrise (multipliserer antall rader i den første ganger antall kolonner i den andre). Legg merke til at BA ikke er definert siden antall kolonner i B ikke matcher antall rader i A.

Matlab:

Vi angir matrisene slik:

>>A=[-1 5 -4 ; 3 2 1];

>>B=[2 1 0 ; 0 -2 1 ; -1 2 3];

>>A*B

Ans =

    2  -19  -7

    5    1   5

Vektor * matrise

Dette er egentlig bare et spesialtilfelle av vanlig matrise-multiplikasjon.

Anta følgende multiplikasjon:

Observer at dette resulterer i en 1*3 radvektor:

Identitetsmatrisa

Dette er en kvadratisk matrise som har verdien 1 i diagonalen og 0 ellers.

M*I = I*M = M

Multiplikasjon med en identitetsmatrise gir ingen endring på opprinnelig matrise.

Inverse matriser

Den inverse av en kvadratisk matrise er definert som A-1 og har følgende egenskap:

A-1 * A = I

der I er identitesmatrisa. For at en kvadratisk matrise skal ha en tilsvarende invers må den ha visse egenskaper.

Dersom man har en rotasjonsmatrise og inverterer den vil den inverse gi en rotasjon i motsatt retning, den inverse av en skaleringsmatrise som skalerer opp en modell vil skalere modellen ned igjen osv.

Eksempel:

Den inverse av følgende matrise (som er en «translasjonsmatrise»)

vil være:

Ting blir mer utfordrende når vi har sammensatte transformasjoner – å finne den inverse blir ikke lenger så enkelt. Inversen kan regnes ut på ulike måter som vi ikke skal gå inn på her siden det normalt vil omfatte en hel forelesning i lineær algebra. Se f.eks. (Weisstein, E.W., 2011) for mer informasjon om inverse matriser.

Transponert matrise

Den transponerte matrisen AT er definert ved at rader i den opprinnelige matrisen A blir kolonner i den transponerte matrisen. Etter hvert vil vi se at «transpornering» og invertering av matriser brukes til å transformere normalvektorer.

2D transformasjoner

Før vi går inn på 3D transformasjoner skal vi så på grunnleggende 2D transformasjoner.

2D-skalering vha. en matrise

Anta at vi har et 2D punkt angitt som (x,y) som skaleres med faktorene a og b. Dette betyr at det skalerte punktet blir (ax, by).

Dette kan settes opp som en matrisemultiplikasjon slik:

Vektoren bak = tegnet tilsvarer nå det skalerte punktet.

2D-rotasjoner vha. matriser

Man kan rotere et punkt (x,y) med en vinkel θ til et punkt (x’, y’) = (x cosθ - y sinθ, x sinθ + y cos θ). Se også figur under.

Teorien bak dette er som følger:

Fra matematikken vet vi at:

Vi vet at x=rcosα og at y=rsinα (der r er lengden på vektorene). Dermed kan vi sette x’ = rcos(α+θ) og y’ = rsin(α+θ). Se figur. Dette multipliseres til uttrykkene for x’ og y’ vist over som til slutt reduseres til x’=xcosθ-ysinθ og y’=xsinθ+ycosθ ved å erstatte rcosα med x og rsinα med y.

Vi kan nå sette dette opp som en matrisemultiplikasjon slik:

2D-translasjon vha. en matrise

Translasjon (forflytning) av et punkt p=(x,y) tilsvarende en gitt vektor v=(s,t) innebærer en vektorsummering:

(x,y) + (s,t) = (x+s, y+t)

Dette bryter med de andre transformasjonene (skalering og rotasjon) som enkelt lar seg uttrykke og kombinere vha. matrisemultiplikasjon:

Skalering:     p’ = Mscale * p

Rotasjon:     p’ = Mrotation * p

Translasjon:     p’ = v + p   (der v er translasjonssvektoren).

Translasjon håndteres med andre ord ulikt de andre transformasjonene.

For å løse dette brukes såkalte homogene koordinater. Dette innebærer at man legger til en ekstra koordinatverdi, w. 2D punktet angis dermed slik: (x,y,w). Dette betyr at tilsvarende kartesiske koordinater blir (x/w, y/w). Dersom w=0 representerer dette et punkt i uendeligheten og bør unngås dersom punktet representerer en lokasjon. Settes w=1 oppnår vi det vi ønsker:

En translasjon tilsvarende

(x,y,1) + (s,t,0) = (x+s, y+t, 1)

kan nå representeres som en matrise slik:

Vi kan nå bruke matrisemultiplikasjon til å translere punkter. Matrisene for skalering og rotasjon utvides på samme måte til 3x3 matriser slik at de tre typene transformasjoner kan håndteres på en ensartet måte.

Dette betyr at man kan lage sammensatte transformasjoner ved å multiplisere matrisene med hverandre – noe som går bra siden alle typer transformasjoner kan representeres av 3x3 matriser.

Eksempel:

Dersom man har en translasjonsmatrise Mt og en rotasjonsmatrise Mr slås disse sammen vha. matrisemultiplikasjon, M = Mt * Mr. Matrisen M kan nå brukes til å transformere vektorene. Eksempel: Vtrans =  v * M.

Transformasjonsmatrisene for 3D

Her vil vi presentere de grunnleggende matrisene som brukes av OpenGL ES og WebGL til å skalere, rotere og translere (forflytte) 3D objekter i rommet. Translasjon i 3D fungerer på samme måte som i 2D ved å bruke homogene koordinater (x,y,z,w).

Skalering fungerer også tilsvarende skalering for 2D. Når det gjelder rotasjon må man i tillegg angi aksen som objektet skal roteres om (x,y eller z).

For å kunne kombinere alle typer transformasjoner vha. matrisemultiplikasjon er også skalering- og rotasjonsmatrisene utvidet til 4x4 matriser.

Skalering

Anta at vi ønsker å skalere en modell til det dobbelte av den opprinnelige modellen. Følgende matrise er definert og brukes til skalering av punkter:

Setter man Sx = 2, Sy = 2 og Sz = 2 skaleres modellen i alle retninger til det dobbelte. Se figuren under:

Skalerer med faktor 2

Rotasjoner

Følgende matrise er definert og brukes til rotasjon rundt x-aksen:

Følgende matrise er definert og brukes til rotasjon rundt y-aksen:

Følgende matrise er definert og brukes til rotasjon rundt z-aksen:

Translasjon og bruk av homogene koordinater

Som vi ser bruker OpenGL ES 4x4 matriser. Dette er (tilsvarende som for 2D) nødvendig for at matrisene skal kunne kombineres med translasjon (forflytning). Poenget er at vi ønsker samme format på matrisene for alle typer transformasjoner slik at det er enkelt å kombinere disse.

Translasjonsmatrisa er definert som følger:

der b tilsvarer forflytning i x,y,z retning.

Eksempel:

Anta at vi har et kvadrat avgrenset av minimumspunktet (-8,2,0) og maksimumspunktet (-2, 8, 0). Anta videre at vi ønsker å translere dette 12 enheter på x-aksen, -10 enheter på y-aksen og 0 på z-aksen. Translasjonsmatrisa blir som følger:

Gjør om punktene til homogene koordinater ved å setter w=1. Dette gir:

Resultatet illustrert:

Translasjon

Bruk av 4x4 matriser gjør det mulig å kombinere transformasjonsmatrisene på en ensartet måte ved hjelp av matrisemultiplikasjon. Skal man gjøre en rotasjon og en translasjon lager man to matriser og multipliserer disse. Dette gir en ny matrise som representerer den totale transformasjonen. Legg merke til at rekkefølgen på matrisemultiplikasjonen er avgjørende (A*B er ulik B*A).

Sammensatte transformasjoner

Som tidligere antydet kan man eksempelvis kombinere en translasjon med en rotasjon – vi lager da en translasjonsmatrise og en rotasjonsmatrise. Vi kombinerer disse vha. en matrisemultiplikasjon.

Legg merke til at rekkefølgen av slike matrisemultiplikasjoner er avgjørende;

A * B ≠ B * A (der A og B er matriser).

Eksempel: Anta at punktet P skal transleres tilsvarende [12,-10,0] og roteres 35 grader om X-aksen.

Her lages to matriser som slås sammen før resultatmatrisa multipliseres med punktet P.  Matrisa Mtranslate_rotateX tilsvarer her produktet av Mtranslate og MrotateX. Punktet P vil i dette tilfellet først transleres og deretter roteres. Resultatet er punktet Ptransformed.

Legg merke til at matrisene kombineres (multipliseres) til en ny matrise før denne multipliseres med punktet. Den nye matrisen representerer begge transformasjonene.

Alternativet er at punktet først multipliseres med translasjonsmatrisa for deretter å multipliseres med rotasjonsmatrisa. Dette vil også fungere men dersom vi skal transformere en modell som består at mange punkter vil dette være lite effektivt da det krever (omtrent) dobbelt så mange matrisemultiplikasjoner i forhold til om matrisene først multipliseres sammen til en ny kombinert matrise. I det første tilfellet må det utføres N*2 vektor/matrise- multiplikasjoner mens det i det andre tilfellet må utføres N vektor/matrise- multiplikasjoner og en matrise/matrise-multiplikasjon (der N=antall punkter).

Mer om sammensatte transformasjoner

Rotasjonsmatrisa som ble presentert i forrige avsnitt sørger for rotasjon om origo. Det er imidlertid ikke alltid at modellen vi operer med er sentrert om origo.

Figuren viser hva som skjer dersom vi roterer tannhjulet når dette ikke er sentrert om origo – det roteres om origo.

Dersom man ønsker at tannhjulet skal roteres om sitt eget sentrum flyttes (transleres) tannhjulet til origo for deretter gjøre rotasjonen og til slutt flytte tannhjulet tilbake. Den komplette sammensatte transformasjonen kan representeres av følgende matrise:

M = Mtrans -1 * Mrot * Mtrans   

Dersom man tegner modellen sentrert om origo slipper man å flytte modellen til origo før rotasjon. Det er derfor ofte lurt å tegne (f.eks. i et tegneverktøy) modellene slik at de er sentrert om origo.

Javascript, WebGL og transformasjonsmatrisene

Som vist over finnes det et sett med ferdigdefinerte transformasjonsmatriser som håndterer translasjoner, rotasjoner og skalering av punkter i rommet.

Her ser vi på hvordan man ved hjelp av eksisterende Javascript-funksjoner og klasser kan generere matrisene i Javascript/WebGL kode. Alternativet er å «håndkode» matrisene (som arrays) – noe som vil oppleves som veldig tungvint.

Her brukes Javascript-biblioteket cuon-matrix.s (Matsuda, K. et al, 2013).

Etter at matrisen er generert sendes den til verteksshaderen som bruker den til å transformere verteksene som «passerer» shaderen. Verteksshaderen er et program som kjøres av GPUen. Her utføres blant annet vektor/matrise-multiplikasjoner. Shadere vil bli mer omtalt etter hvert.

Translasjonsmatrisa:

Denne sørger for å flytte et punkt i forhold til verdiene på bx,by og bz.

Multipliserer vi et punkt med denne matrisa vil punktet forflytte seg tilsvarende verdien på disse. Dersom p1 = (1,2,3) og vi setter bx = 2, by = 2 og bz = 2 og multipliserer med matrisa får vi den transformerte vektoren p2 = (3,4,5).

let bx = 2, by=2, bz=2;

let modelMatrix = new Matrix4();

modelMatrix.setTranslate(bx, by, bz);

Matrisen modelMatrix vil nå se slik ut:

Dersom man studerer modelMatrix-objektet vil vi se at det består av et array, elements, med plass til 16 elementer med indeks f.o.m. 0 t.o.m. 15. I forhold til matrisa over tilsvarer de 4 (indeks 0-3) første elementene 1. kolonne i matrisa, de fire neste (indeks 4-7) 2. kolonne osv. Elements-tabellen vil i dette tilfellet se slik ut:

    [1,0,0,0,0,1,0,0,0,0,1,0,2,2,2,1]

Det samme gjelder for de andre matrisene som omtales under.

Rotasjonsmatriser:

Her har vi tre matriser, en for rotasjon rundt hver av aksene. Det er også mulig å rotere rundt en vilkårlig vektor.

Eksempel på hvordan man generere en slik matriser vha. Javascript-funksjoner:

let angle = 60;    //i grader

let modelMatrix = new Matrix4();

modelMatrix.setRotate(angle, 0, 1, 0);

Her oppretter vi en rotasjonsmatrise, modeMatrix, som vil rotere punkter 60 grader om y-aksen. På samme måte kan vi lage matriser for rotasjon rundt Y og Z-aksen evt. vilkårlig vektor vha. de tre siste parametrene til setRotate().

Skaleringsmatrise:

Vi oppretter en skaleringsmatrise slik:

let scaleX = 0.5, scaleY = 0.5, scaleZ = 0.5;    //halvverer i alle retninger

let modelMatrix = new Matrix4();

modelMatrix.setScale(scaleX, scaleY, scaleZ);

Legg merke til at forskjellen i forhold til translasjon er at vektorkomponentene multipliseres med verdiene i skaleringsmatrisa. Ved translasjon adderes vektorkomponentene til matriseverdiene.