Modul 5.1: Lys og lysberegning, introduksjon

Introduksjon

Vi har hittil sett hvordan vi legger farge og tekstur på 3D modellene. Dette gir greie modeller men fortsatt mangler det noe for å få skikkelig 3D effekt.

Belysning er kanskje det viktigste momentet for å få 3D modeller til å fremstå realistiske. Uten belysning vil 3D-modeller og scener i enkelte tilfeller fremstå som 2D. Et eksempel på dette er en kule konstruert av et antall trekanter. Uten lyseffekter vil denne fremstå som en 2D sirkel. Med korrekt belysning vil den delen av kula som står mot lyset fremstå med klarere farge enn den som er vendt fra lyset.

I denne sammenheng ønsker vi, på best mulig måte, å simulere hvordan lys fra ulike kilder påvirker fargen til objektene/modellene. Nøyaktig simulering av hva som skjer i den virkelige verden er krevende siden lys kan komme fra mange kilder og retninger og ikke minst at lyset reflekteres og absorberes fra de fleste objekter/flater som det treffer. Ulike lysstråler kan dermed komme fra «alle kanter» med et utall av innfallsvinkler, intensitet og farge .

Det gjøres derfor en del forenklinger for at det skal være mulig å simulere lys på en fornuftig måte. Forenkling er spesielt viktig i spill som kjører en «game loop» og dermed må utføre slike beregninger normalt ca. 60 ganger i sekundet.

3D modeller og «shading»

Hvilken farge et objekt i den virkelige verden fremstår med er avhengig av lysets farge og retning samt hvilket materiale objektet er laget av. Lyset treffer objektet, det reflekteres og «treffer» våre øyne som, vha. hjernen, oppfatter objektets farge. En boks som belyses med hvitt lys vil fremstå med ulike farger avhengig av hva boksen er laget av og hvilken type lys (spotlys, sol o.l.) boksen belyses med.

I den virkelige verden er det to fenomener som inntrer når et objekt belyses:

1. Objektets overflate farge/skyggelegges i forhold til lysets farge og retning samt materialet boksen er laget av.
2. Objektet vil kaste skygge avhengig av lyskilden og retninga.

Forskjellen på shading & «kaste skygge»

Det første av disse punktene (1) omhandler det som på engelsk kalles «shading». Begrepet kan oppfattes som noe diffust siden det på norsk direkte oversatt betyr noe sånt som «skyggelegging». I 3D datamaskingrafikk handler shading om å gi objektenes ulike sider forskjellige farger basert på lysfarge, materiale og lysretning.

Et eksempel: Som vist i figuren over fremstår boksens ulike flater med litt forskjellige fargenyanser avhengig av hvor lyset kommer fra og fra hvilken vinkel boksen betraktes. Boksens sider er ulikt farge/skyggelagt – herav begrepet «shading».

Shading er såpass fundamentalt i forbindelse med 3D grafikk at språket som man programmerer GPUen/pipelinen med kalles “shading language”. Sammen med WebGL brukes GLSL ES (Khronos Group, GLSL ES, 2009) som står for Open GL ES Shading Language. Det opprinnelige poenget med verteks og fragment- shadere var å utføre shading, dvs. beregne pikslenes farger vha. lysfarger, lysretning m.m.

Punkt 2 over omfatter det å vise skygge av et objekt. Det er selvfølgelig mulig å generere og vise skygger av 3D-modeller men dette vil ikke bli omtalt her.

Oversikt

Følgende begreper er sentrale i forbindelse med lys og lysberegning:

• Lokal eller global belysningsmodell.
• Materialegenskaper
• Lys og lysberegning
• Ulike typer lyskilder:

• Retningsorientert lys
• Punktlys
• Spotlight
• Ambient lys

• Phong reflection model.
• Fargen til et objekt bestemmes av lyset som reflekteres fra modellen. 
• Reflektert lys deles inn i følgende refleksjonskomponenter:
• Ambient
• Diffuse
• Specular
• Interpoleringsteknikker: Bestemmer hvordan lysberegninga gjøres. Varianter:
• Flat shading (per flate/trekant)
• Gourad shading (per verteks)
• Phong shading (per fragment).

• Begrepet shading omfatter det å beregne fargen til et punkt, et primitiv (trekant) eller objekt/modell basert på:
• Lyskildenes posisjon og avstand
• Fargen på lyset
• Materialegenskaper
• Kameraets posisjon
• Normalvektorer

• Invers-transponert modelview-matrise brukes til å transformere normalvektorer.

Disse begrepene omtales i påfølgende kapitler.

Lokal eller global lysmodell

I forbindelse med spillutvikling brukes som regel en såkalt lokal belysningsmodell, local illumination model (Luna, F. D., 2006) som betyr at hvert objekt belyses uavhengig av hverandre og der man kun tar hensyn til lyset som kommer direkte fra lyskilden. Reflektert lys fra andre modeller ignoreres dermed ved beregning av lys. Dette forenkler beregningene og er illustrert i figuren under. Selv om kula til venstre egentlig skjuler den andre kula får de samme belysning.

Lokal belysningsmodell

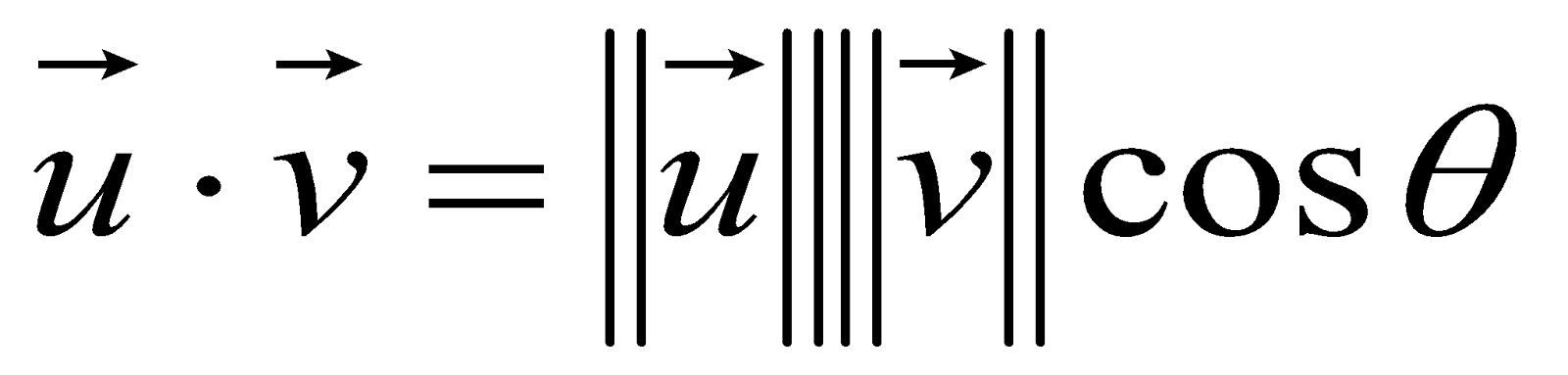
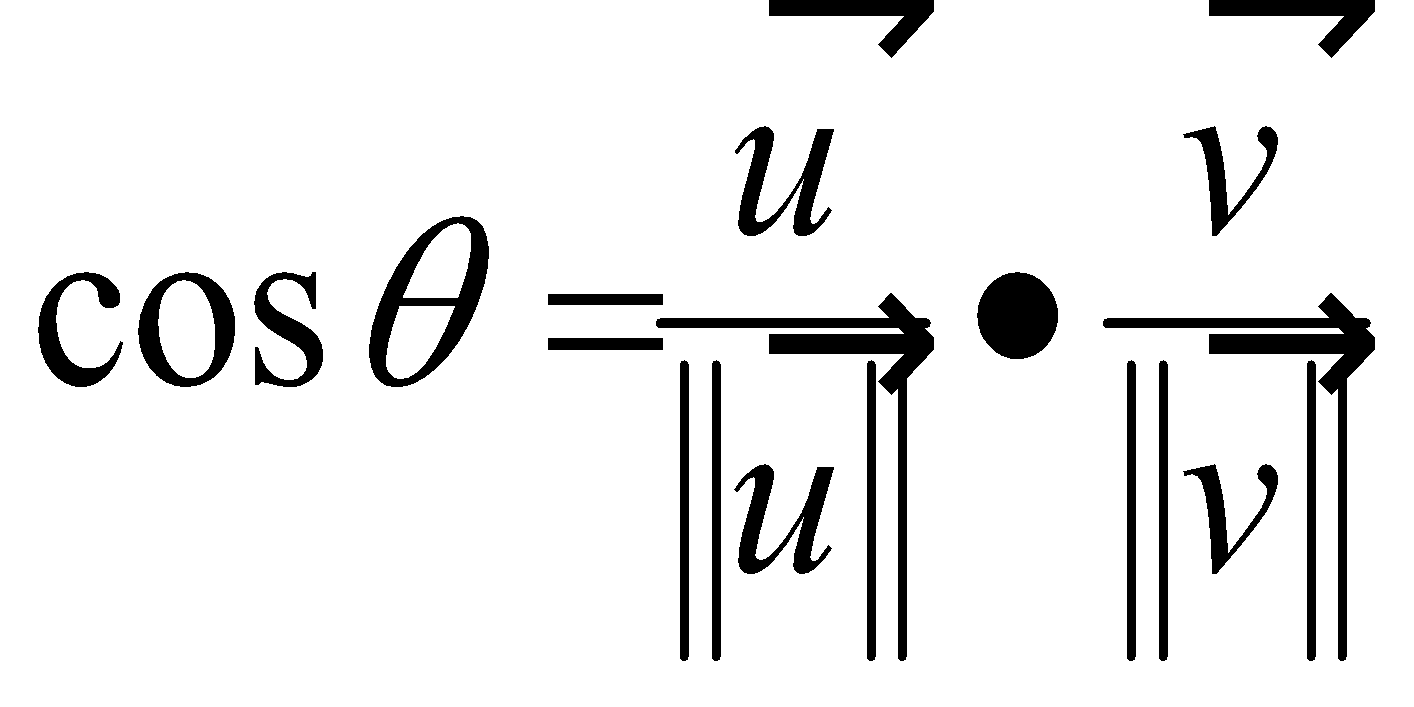
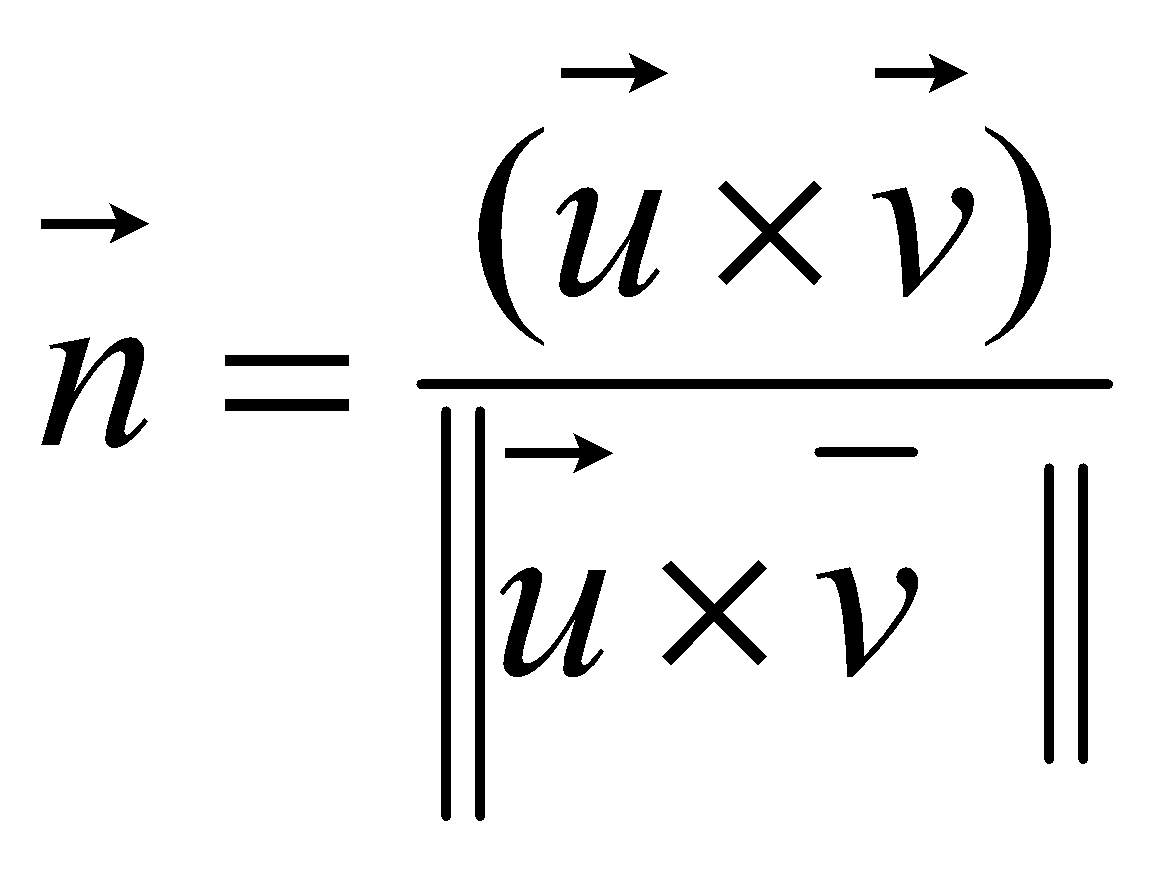
Et eksempel på en lokal belysningsmodell er «Phong reflection model» (Phong, B.T, 1975) (Anyuru, A., 2012). Denne modellen brukes normalt i sanntids spill omtales derfor i eget kapittel under.

Alternativt vil man i en global belysningsmodell (global illumination model) også ta hensyn til lys som reflekteres fra alle andre objekter i scenen. Slike modeller er naturlig nok mer beregningskrevende og mindre aktuell i 3D sanntidsspill.

Eksempel på en global belysningsmodell er ray tracing som kan produsere fotorealistiske bilder. Siden dette er en beregningskrevende teknikk benyttes dette som regel der bildet «rendres» i god tid før det vises på skjermen som f.eks. til stillbilder og/eller film.

Lys og materialegenskaper

Når vi bruker lysberegning trenger man ikke sette farge på hver enkelt verteks selv om det også er mulig å blande verteksfarge med beregnet lysfarge.

Fargene kan i stedet bestemmes ved å spesifisere lys- og materialegenskaper. Verteks- og/eller fragmentfargene beregnes så vha. disse egenskapene.

Eksempler på materialegenskaper er hvilke farger som reflekteres eller absorberes fra en belyst overflate, materialets gjennomsiktighet og evt. gjenskinn.

Lys modelleres vha. en blanding av tre farger; rød, grønn og blå (RGB – Red, Green, Blue). Når lys går fra en lyskilde mot et objekt vil noe av lyset reflekteres og noe absorberes. Dersom objektet er gjennomsiktig, for eksempel glass, vil deler av lyset passere gjennom objektet. I den virkelige verden vil også de ulike objektene belyses med reflektert lys fra andre objekter, vegger osv.

Det reflekterte lyset ender opp hos betrakteren (øyet). Det menneskelige øye skiller på rødt, grønt og blått lys av varierende styrke. Dette hjelper hjernen å danne et bilde basert på lysreseptorene i øyet.

Refleksjon og absorbsjon av hvitt lys

Figuren viser hvordan hvitt, retningsorientert lys (a), reflekteres fra og absorberes av sylinderen og kula før det treffer øyet.

Anta for eksempel at materialet som sylinderen er laget av reflekterer 75% av rødt lys, 75 % av grønt lys og absorberer resten (b). Alt blått lys vil dermed absorberes. Betrakteren vil dermed oppfatte sylinderen som gul (blanding av rødt og grønt).

Kula reflekterer 25 % (c) av det røde lyset og absorberer resten. Kula vil dermed fremstås som (mørk) rød for betrakteren. I virkeligheten vil også noe lys reflekteres fra sylinderen og treffe kula, og motsatt.

I den virkelige verden er det med andre ord materialet et objekt er laget av, eller kledd/dekt med, som bestemmer hvilket lys, og dermed farge, som reflekteres. En agurk oppfattes som grønn fordi overflaten har fysiske egenskaper som gjør at den reflekterer den grønne delen av lysspektret.

Lys angis ofte som en RGB-verdi, f.eks. [1.0, 1.0, 1.0] for hvitt lys. Det samme gjelder materialegenskapen, f.eks. [0.75, 0.75, 0.0] (for sylinderen i figuren over).

Resultatfargen er en komponentvis multiplikasjon:

farge * materiale =

[1.0, 1.0, 1.0] * [0.75, 0.75, 0.0] =

[1.0 * 0.75, 1.0 * 0.75, 1.0 * 0.0,] =

[0.75, 0.75, 0.0]

som gir gul farge.

Lys og lysberegning

I forbindelse med «shading» av objekter er følgende essensielt:

• Type lyskilde som benyttes.
• Hvordan lyset reflekteres fra flatene til objektet, dvs. hvilken belysningsmodell som brukes.

Typer lyskilder

I 3D datamaskingrafikk opererer man gjerne med følgende typer lyskilder:

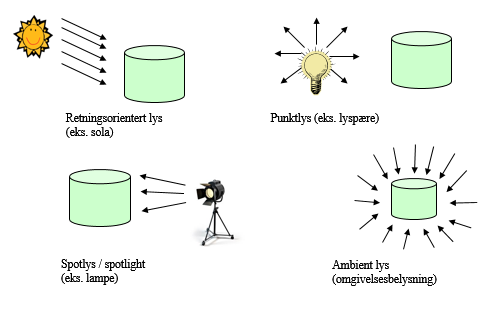
• Retningsorientert lys  
• Parallelle innkommende lysstråler, simulerer sollys
• Punktbelysning
• Simulerer for eksempel en lyspære der lyset stråler i alle retninger
• Spotlys / spotlight
• Simulerer en fokusert lyskjegle, eks. lommelykt, gatelykt, billys m.m.
• Ambient
• Indirekte lys / omgivelsesbelysning. Dette er egentlig ikke en kilde i seg selv men i stedet et resultat av alle andre lyskilder. Ambient lys har ingen retning. Alle modeller og sider belyses likt fra alle kanter.

Figuren under viser forskjellen på disse.

Ulike typer lys

I forbindelse med WebGL simuleres slike lystyper ved å gjøre ulike beregninger i verteks- og/eller fragmentshaderen.

Retningsorientert lys er lys med kilde som vi antar er uendelig langt unna slik at lysstrålene faller parallelt inn mot objektene. Vi kan sammenlikne dette med sollys. Når vi bruker retningsorientert lys bruker vi en «lysvektor» til å angi retninga. Dette betyr at man kan bruke samme vektor for alle verteksene (og/eller fragmentene) til en modell når man gjør lysberegning.

Punktlys har en posisjon og utstråler lys i alle retninger fra dette punktet. Eksempel på punktlys er en lyspære uten skjerm. Innfallsvinkelen mellom lyset og objektet vil variere fra verteks til verteks og lysvektoren må beregnes for hver verteks (evt. fragment).

Et spotlys avgir et koneformet lys med en bestemt retning. Eksempler på spotlys er en lampe med skjerm, et frontlysene til en bil o.l.

Geometrien til spotlys.

Figuren viser geometrien som man må kjenne til for å kunne beregne og simulere spotlys. Mer om dette etter hvert.

Ambient lys: Dette er en type lys som alltid er til stede i en scene – en form for bakgrunnsbelysning som kommer fra alle kanter og er til stede pga. refleksjoner fra alle andre lyskilder.

Phong reflection model

Tidligere har vi sett hvordan vi kan knytte en fargeverdi (RGBA) direkte til en verteks. På veien mellom verteks- og fragmentshaderen interpoleres verteksfargene slik at hvert fragment til en trekant får farge basert på en interpolert verdi.

I stedet for å angi farge for hver verteks kan fargen kalkuleres i verteksshaderen basert på diverse lysparametre som normalvektor, lysretning, lysfarge osv. Dette betyr at verteksshaderen må motta slike verdier/parametre (i tillegg til verteksposisjon) for å kunne beregne verteksfarge.

Alternativt kan slike parametre, f.eks. lysvektoren, videresendes (vha. en varying) til fragmentshaderen slik at disse også interpoleres lineært. Hvert fragment har da, eksempelvis, en lysvektor som kan benyttes til å beregne lysfarge for dette fragmentet.

«Phong reflection model» ble utviklet av Bui Tuong Pong og publisert i 1975 (Phong, B.T. 1975) og er en lokal belysningsmodell. Her er det viktig å innse at fargen til et objekt bestemmes av fargen til lyset som reflekteres fra modellen. Et rødt objekt fremstår, i den virkelige verden, som rødt fordi overflaten har fysiske egenskaper som gjør at det reflekterer det røde lyset.

Modellen, som også kalles «ADS lysmodell», er basert på at resultatfargen til en verteks, eller et fragment, er summen av følgende refleksjonskomponenter:

• Ambient refleksjon (omgivelsesrefleksjon)
• Diffuse refleksjon (spredt refleksjon) og
• Specular refleksjon (speilrefleksjon)

Resultatfargen (totalrefleksjon) til et punkt, verteks eller fragment, kan beskrives som summen av de nevnte refleksjonskomponentene, slik:

Totalrefleksjon = ambient refleksjon + diffus refleksjon + speilrefleksjon

For å kunne beregne disse tre komponentene brukes følgende tre lyskilder:

• Ambient lys (omgivelseslys),
• Diffuse lys («spredt»/diffust lys) og
• Specular lys («speilglanslys»).

I tillegg angis «materialet» som objektene består av vha.

• ambient,
• diffus og
• specular materialegenskaper

Ambient refleksjon, i likninga over, beregnes med andre ord vha. ambient lys og ambient materialegenskap. Ambient refleksjon tilsvarer da fargen som ambient lys og ambient materialfarge til sammen utgjør. Disse slås sammen vha. komponentvis multiplikasjon som vist tidligere.

Tilsvarende for diffuse og specular refleksjon. Diffus refleksjon tilsvarer fargen som diffus lysfarge og diffus materialfarge til sammen utgjør mens speilrefleksjon tilsvarer fargen som specular lysfarge og specular materialfarge til sammen utgjør.

Her er det mange begreper ute og går – det som er viktig er at «ambient refleksjon» omfatter lys og materialegenskaper. Begge disse angis som en fargevektor bestående av en rød, en grønn og en blå-komponent (RGB).  Det betyr at både lys og materialegenskap angis som RBG-verdier, dvs. 3 flyttallverdier i området 0 - 1. Disse slås så sammen vha. komponentvis multiplikasjon.

Eksempel: Anta ambient lys = [1,1,1] og at dette belyser et objekt med materialegenskap = [0.4, 1.0, 0.0]. Ambient refleksjon blir da produktet av disse, som vil bli [0.4, 1.0, 0.0]. Dette indikerer at 40% av innkommende rødt lys reflekteres mens 60% absorberes. Alt grønt lys reflekteres mens alt blått lys absorberes. Ofte anngis et slikt lys som en lysvektor, altså som en sammenslått verdi (og ikke både lys og materialvektor). I dette tilfellet [0.4, 1.0, 0.0].

Ambient refleksjon

Ambient lys, eller omgivelsesbelysning, er lys som alltid er til stede i en scene – en form for bakgrunnsbelysning som kommer fra alle kanter. Dette er uavhengig av objektenes orientering og plassering i forhold til andre lyskilder. Alle deler av modellen belyses likt med dette lyset.

For å kunne beregne ambient refleksjon angis ambient lys, Ia, og ambient materialegenskap, ka. Disse slås sammen og gir ambient refleksjon.

ambient relfleksjon = ka * Ia

Ambient refleksjon tilsvarer da fargen som utgjøres av omgivelsesbelysning og materialegenskapen til objektet som belyses.

Dette implementeres for eksempel ved å sende disse to verdiene til verteksshaderen, som slår disse sammen:

uniform vec4 uAmbientMaterial;

uniform vec4 uAmbientColor;

. . .

vec4 ambientReflection = uAmbientMaterial * uAmbientColor;

Denne verdien, ambientReflection, summeres så typisk med tilsvarende for «diffuse» og «specular»-komponentene. Beregnet farge sendes deretter videre til fragmentshaderen via en varying-parameter (slik at fargen interpoleres).

En verteksshader som kun håndterer ambient-lys vil kunne se slik ut:

<!-- SHADER som håndterer posisjon og lys. -->
<script id="ambient-vertex-shader" type="x-shader/x-vertex">
    attribute vec3 aVertexPosition;
    uniform vec4 uAmbientMaterial;
    uniform vec4 uAmbientColor;
    uniform mat4 uModelViewMatrix;
    uniform mat4 uProjectionMatrix;
    varying vec4 vAmbientLight;
    void main() {
        vec4 ambientReflection = uAmbientMaterial * uAmbientColor;
        vAmbientLight = ambientReflection;
        gl_Position = uProjectionMatrix * uModelViewMatrix * vec4(aVertexPosition, 1.0);
    }
</script>

Fragmentshaderen vil da kunne se slik ut:

<script id="ambient-fragment-shader" type="x-shader/x-fragment">
    precision mediump float;
    varying vec4 vAmbientLight;
    void main() {
        gl_FragColor = vAmbientLight;
    }
</script>

Legg merke til at verteksshaderen tar inn posisjon (aVertexPosition) men ingen farge. Fargen beregnes her ved å slå sammen uniform-parametrene uAmbientMaterial og uAmbientColor vha, en komponentvis multiplikasjon.

Bruk av en verdi for ambient refleksjon

I praksis opererer man ofte med en fargeverdi (vektor) for ambient refleksjon, en for diffuse refleksjon og en for specular refleksjon. Vi kan f.eks. slå sammen lys- og materialfarge i Javascript-koden, evt. bare bruke en verdi og anta at dette er sammenslått lys og materialfarger, før den sendes til shaderen.

Foreløpig ser vi kun på ambient og følgende kode viser bruk av en fargeverdi for ambient refleksjon. Her kaller vi den uAmbientLightColor.

Verteksshaderen blir da enda enklere (varying-variabelen er nå navngitt vLight):

<script id="ambient-vertex-shader" type="x-shader/x-vertex">
    attribute vec3 aVertexPosition;
    uniform vec4 uAmbientLightColor;
    uniform mat4 uModelViewMatrix;
    uniform mat4 uProjectionMatrix;
    varying vec4 vLight;
    void main() {
        vLight = uAmbientLightColor;
        gl_Position = uProjectionMatrix * uModelViewMatrix * vec4(aVertexPosition, 1.0);
    }
</script>

Tilhørende fragmentshader:

<script id="ambient-fragment-shader" type="x-shader/x-fragment">
    precision mediump float;
    varying vec4 vLight;
    void main() {
        gl_FragColor = vLight;
    }
</script>

I javascript-koden må uAmbientLightColor gis verdi på samme måte som vist tidligere. Bruk av kun ambient lys vil f.eks. kunne gi følgende resultat (dersom uAmbientLight er tilordnet en gråfarge):

Kuben belyst med kun omgivelsesbelysning

Som vi ser er 3D-effekten fraværende. Siden alle sider belyses likt vil alle fragmenter få samme fargeverdi. Ambient lys alene vil ikke gi tilfredsstillende 3D-resultat. Dette brukes kun til å heve totalbelysningen. Husk at totalbelysning(/refleksjon) beregnes slik:

    Totalrefleksjon = ambient refleksjon + diffuse refleksjon + specular refleksjon.

Vi har i foregående eksempel kun beregnet første del av denne likninga. I neste avsnitt ser vi på diffus refleksjon. 

Diffus refleksjon

Diffust lys er lys som har en retning, dvs. som kommer fra en lyskilde. Dette kan være retningsorientert lys eller punktlys. Ved beregning av diffus refleksjon må man ta hensyn til innfallsvinkelen til lyset. Lys som står vinkelrett mot en flate vil reflektere mer lys enn lys som faller skrått mot en flate.

Diffus belysning – tar hensyn til lysets innfallsvinkel

Til venstre i figuren er dette illustrert vha. et punktlys. Her er det indikert at lys som treffer vinkelrett på flaten gir en mer opplyst flate enn lysstråler som med innfallsvinkel ulik 90 grader. Det samme er tilfelle for retningsorientert lys, stråler med innfallsvinkel ulik 90 grader gir en svakere belyst flate.

Ved diffus refleksjon vil det reflekterte lyset spres likt i alle retninger. Dette betyr igjen at resultatfargen er uavhengig av hvor kameraet står, dvs. hvor objektet betraktes fra. Som vi etter hvert vil se har kameraets posisjon derimot avgjørende betydning i sammenheng med speilrefleksjon (specular reflection). Matte og bleke materialer som leire, sand, kalk o.l. gir diffus refleksjon.

 

Diffus refleksjon.

Før vi går videre og beregner diffust lys må vi diskutere normalvektoren.

Normalvektor

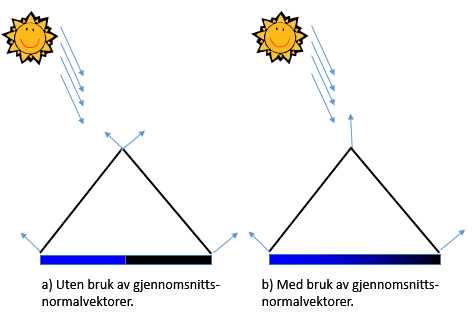
Figuren under illustrerer hvordan belysningen på en flate varierer med innfallsvinkelen til lyset. Vi ser her et rektangel, tegnet vha. to trekanter, som gradvis retter seg opp mot lyset.  

Belysning av et rektangel (Riemer, G. "Experimenting with Lights in XNA", 2011)

Når rektanglet ligger flatt (”på bakken”) vil ikke noe lys treffe flaten og den vil derfor vises som mørk. Etter hvert som rektanglet retter seg opp slik at lyset treffer bedre vil flaten fremstå med klarere og klarere farge. Strekene som peker ut fra rektanglet indikerer normalvektorer knyttet til verteksene. Lyset treffer altså flatene med ulike innfallsvinkler.

Figuren under viser hvordan lyset treffer tre ulike flater (sett ovenfra) og hvordan normalvektoren er med på å bestemme hvor mye av lyset som skal reflekteres.

Dersom lyset skinner mot de tre flatene skal flate nr 1 reflektere mer lys enn flate 2 og 3. De røde linjene indikerer hvor mye lys som reflekteres fra de ulike flatene. Vi ser at den røde linja fra flate 3 er mindre enn tilsvarende fra flate 2 og 3. Størrelsen på disse (tenkte) linjene kan beregnes dersom WebGL får opplysning om de vinkelrette pilene – normalvektorene – som peker fra hver flate.

Lys og normalvektoren (Riemer, G. "Experimenting with Lights in XNA", 2011)

Normalvektorene knyttes, på samme måte som verteksfarger, til verteksene. Hver trekant vil dermed bestå av tre verteksposisjoner og tilhørende normalvektor.

For å kunne beregne diffus refleksjon må man med andre ord ha normalvektoren til flaten som verteksen er med på å definere. Normalvektoren er i enkelte tilfelle enkel å beregne mens i andre tilfeller er dette mer krevende.

Lamberts lov

Diffus refleksjon kalles også «Lambertion reflection» pga. bruk av Lamberts cosinus-lov ([WikiPedia/Lambert], (Luna, F.D. 2006)) som forklares her.

Lys som treffer en overflate direkte (vinkelrett) vil belyse flaten mer enn lys som treffer flaten med en vinkel. Figuren under illustrerer dette.

Refleksjon i forhold til lysets innfallsvinkel (Luna, F.D., 2006)

Flaten mottar mest lys når lysvektoren L og normalvektoren n er parallelle – dvs. lyset skinner direkte på flaten.  Flaten mottar mindre lys jo større vinkel det er mellom disse vektorene.

Poenget er å finne en funksjon som returnerer ulik intensitet basert på vinkelen mellom verteksnormalen (n) og lysvektoren (L). Legg merke til at vektoren L peker i motsatt retning i forhold til lysets retning.

Funksjonen må returnere maks intensitet når n og L er parallelle dvs. vinkelen mellom dem er lik 0. Intensiteten skal avta etter som vinkelen øker. Når vinkelen passerer 90 grader belyses baksiden og intensiteten må da settes lik 0.

Lamberts cosinus-lov (Luna, F.D., 2006) gir oss dette:

Der både L og n er enhetsvektorer (normalisert). Her brukes prikk (dot) produktet for å finne vinkelen mellom vektorene L og n.

Generelt beregnes prikkproduktet mellom to vektorer 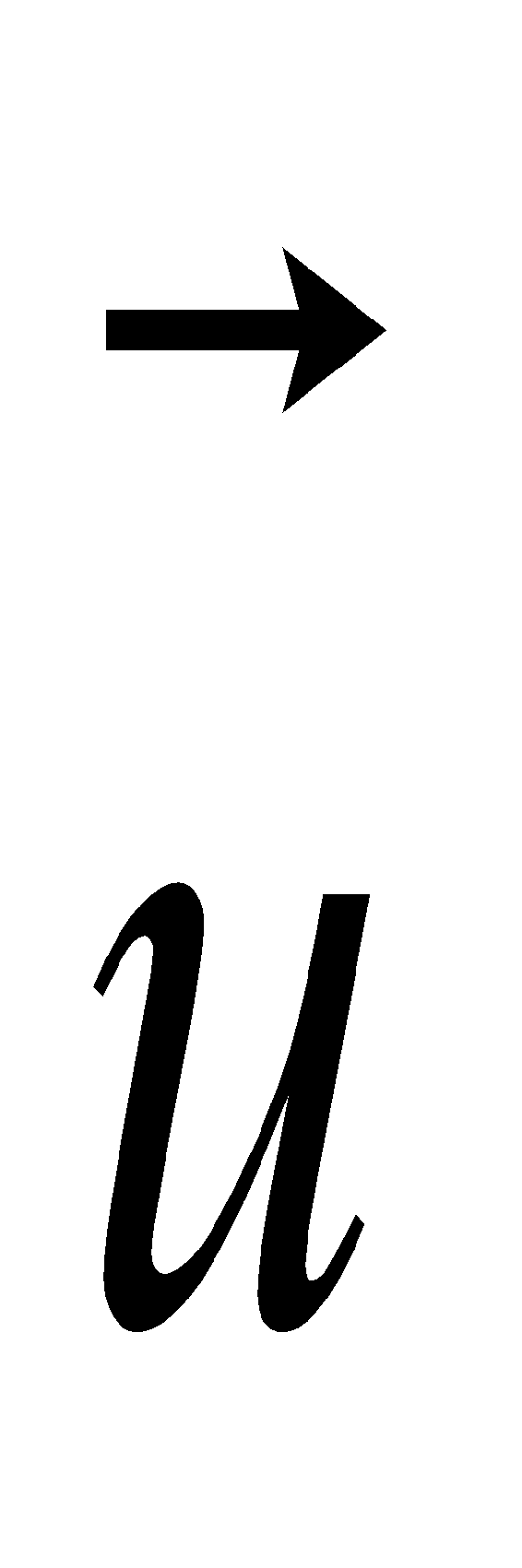og slik:

I dette tilfellet tilsvarer u og v henholdsvis L og n. Så lenge L og n er enhetsvektorer (normalisert) er cosθ lik prikkproduktet mellom disse:

L settes typisk lik normalisert lysvektor multiplisert med (-1).  

Beregne normalvektor: flatenormal og verteksnormal

En flatenormal er en enhetsvektor som står vinkelrett på et polygon (en flate) og dermed beskriver polygonets retning.

Flatenormal

Flatenormalen til en trekant tilsvarer normalisert kryssprodukt mellom to av trekantens «kantvektorer». Dette gir en vektor med lengde = 1 som står vinkelrett på trekanten.

Normalvektoren for trekanten dannet av p0, p1 og p2

Anta en trekant beskrevet av tre punktvektorer, p0, p1 og p2 som vist over. Normalvektoren i p0 kan beregnes slik:

Vektorene u og v beregnes lik:

Vi bruker deretter kryssproduktet til å beregne en normalvektor til flaten (trekanten) definert av disse vektorene. Resultatet normaliseres, slik at lengden til n blir 1:

n er nå en normalisert normalvektor for trekanten. Denne vektoren, n, kan nå tilordnes som normalvektor til verteksene som definerer trekanten.

Problemet med å beregne normalvektor på denne måten i et større mesh er at overgangene mellom de ulike trekantene vil vises tydelig. Grunnen er at alle piksler innafor samme trekant får samme farge og man får dermed et skarpt fargeskille mellom hver enkelt trekant. Dette  kalles flat shading.

For å få en jevnere belysning/refleksjon («shading») kan normalene beregnes per verteks i stedet for per trekant. Som vi skal se etter hvert kan man også gjøre lysberegning per fragment.

Når normaler beregnes per verteks tar man hensyn til flatene som deler samme verteks.

Gjennomsnittsnormalvektor til et mesh med delt verteks

Figuren viser et mesh bestående av 4 trekanter og hvordan disse deler en av verteksene. Normalvektoren, v, er gjennomsnittet av flatenormalene for de 4 trekantene. Vektoren v23 er her beregnet vha. vektorene v2 og v3, v34 er beregnet av vektorene v3 og v4 osv. Brukes nå vektoren v som normalvektor i den delte verteksen for alle de fire trekantene får man en jevnere belysning.

Et annet eksempel: Anta at vi har to flater (sett fra siden) som belyses som vist under.

Normalvektorer i delt verteks (basert på (Riemer, G. "Experimenting with Lights in XNA", 2011))

Dersom verteksene til flatene bruker flatenormalene vil det oppstå et klart fargeskille på flatene som vist til venstre i figuren (a). Dette kalles, som nevnt, flat shading.

Dersom man i stedet beregner og bruker gjennomsnittsnormalvektorer på de verteksene som er delt av flatene vil fargene få en jevnere overgang. Dette ser vi i høyre del av figuren (b). Dette kalles Gourad eller Phong shading avhengig av om lysberegninga utføres i verteks- eller fragmentshaderen. Mer om dette etter hvert.

Figuren under viser flatene ovenfra:

Til venstre: Flat shading. Til høyre: Gourad eller Phong-shading.

Noen ganger ønsker man å bruke flatenormalene uten å beregne gjennomsnittet mens i andre tilfeller må man beregne gjennomsnittet for at resultatet skal blir brukbart. Et eksempel er en kule bestående av mange trekanter. Dersom man ikke bruker gjennomsnittsnormalvektorer vil kulens trekanter bli veldig synlig, brukes gjennomsnittsnormalvektorer får kulen en jevnere overflate.

Ved å gjennomløpe alle trekanter til en modell (et «mesh») og beregne flatenormalen (som forklart over) til hver enkelt trekant kan gjennomsnittsnormalvektoren beregnes i delte vertekser. Hver verteks tilordnes så beregnet gjennomsnittsnormalvektor. Se (OpenGL Wiki, Calculating surface normal, 2013).

Dersom man skal tegne en kube vil det som regel være greit å bruke flatenormalen, som står 90 grader på hver side, til sidenes vertekser. Man trenger i dette tilfellet ikke beregne gjennomsnittsnormalvektor. Se neste avsnitt.

Normalvektorer til en kube

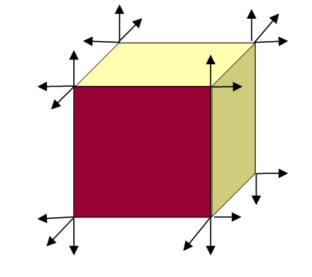
En kube med skarpe kanter vil ha klare fargeforskjeller på sidene. Det er derfor enkelt å finne normalvektorene til kubens sider – disse står vinkelrett på hver side.

Flatenormaler til en kube

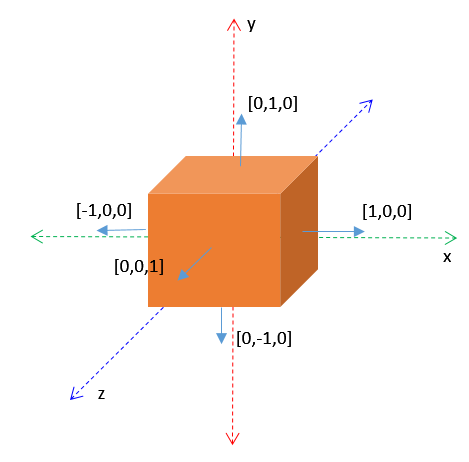
Her vil det være 6 forskjellige normalvektorer som står vinkelrett på flatenes sider. Korrekt normalvektor knyttes til hver enkelt verteks som definerer kuben. Dersom f.eks. høyre siden av kuben er definert av 4 vertekser, assosieres disse verteksene med flatenormalen til kubens høyre side (som i dette tilfellet vil være [1,0,0]).

Normalvektorer knyttet til kubens vertekser.

Figuren viser at det må knyttes en normalvektor, her flatenormalen vil hver side, til hver enkelt verteks.

Knytte normalvektorer til verteksene

Tidligere har vi sett hvordan man assosierer farge med vertekser ved at det opprettes et eget fargebuffer som fylles med fargedata, i form av en RGBA-verdi, per verteks. På samme måte må man assosiere en normalvektor per verteks for å kunne gjøre lysberegninger.

Dersom vi tar utgangspunkt i en kube vil verteksposisjoner f.eks. kunne defineres slik:

function cubePositions() {
   return [
      //Forsiden (pos):
      -1, 1, 1,
      -1, -1, 1,
      1, -1, 1,

      -1, 1, 1,
      1, -1, 1,
      1, 1, 1,

      //Høyre side:
      1, 1, 1,
      1, -1, 1,
      1, -1, -1,

      1, 1, 1,
      1, -1, -1,
      1, 1, -1,

      //Baksiden:
      1, -1, -1,
      -1, -1, -1,
      1, 1, -1,

      -1, -1, -1,
      -1, 1, -1,
      1, 1, -1,

      //Venstre side:
      -1, -1, -1,
      -1, 1, 1,
      -1, 1, -1,

      -1, -1, 1,
      -1, 1, 1,
      -1, -1, -1,

      //Topp:
      -1, 1, 1,
      1, 1, 1,
      -1, 1, -1,

      -1, 1, -1,
      1, 1, 1,
      1, 1, -1,

      //Bunn:
      -1, -1, -1,
      1, -1, 1,
      -1, -1, 1,

      -1, -1, -1,
      1, -1, -1,
      1, -1, 1
   ]
}

Tilsvarende verteksnormaler defineres f.eks. slik:

function cubeNormals() {
   return [
      //Forsiden:
      0.0, 0.0, 1.0,
      0.0, 0.0, 1.0,
      0.0, 0.0, 1.0,

      0.0, 0.0, 1.0,
      0.0, 0.0, 1.0,
      0.0, 0.0, 1.0,

      //Høyre side:
      1.0, 0.0, 0.0,
      1.0, 0.0, 0.0,
      1.0, 0.0, 0.0,

      1.0, 0.0, 0.0,
      1.0, 0.0, 0.0,
      1.0, 0.0, 0.0,

      //Baksiden:
      0.0, 0.0, -1.0,
      0.0, 0.0, -1.0,
      0.0, 0.0, -1.0,

      0.0, 0.0, -1.0,
      0.0, 0.0, -1.0,
      0.0, 0.0, -1.0,

      //Venstre side:
      -1.0, 0.0, 0.0,
      -1.0, 0.0, 0.0,
      -1.0, 0.0, 0.0,

      -1.0, 0.0, 0.0,
      -1.0, 0.0, 0.0,
      -1.0, 0.0, 0.0,

      //Topp
      0.0, 1.0, 0.0,
      0.0, 1.0, 0.0,
      0.0, 1.0, 0.0,

      0.0, 1.0, 0.0,
      0.0, 1.0, 0.0,
      0.0, 1.0, 0.0,

      //Bunn:
      0.0, -1.0, 0.0,
      0.0, -1.0, 0.0,
      0.0, -1.0, 0.0,

      0.0, -1.0, 0.0,
      0.0, -1.0, 0.0,
      0.0, -1.0, 0.0
   ];

}

Posisjon- og normalvektorbuffer opprettes slik:

function initCubeBuffers(gl) {
   let positions = cubePositions();
   let normals = cubeNormals();

   const positionBuffer = gl.createBuffer();
   gl.bindBuffer(gl.ARRAY_BUFFER, positionBuffer);
   gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(positions), gl.STATIC_DRAW);
   gl.bindBuffer(gl.ARRAY_BUFFER, null);

   const normalBuffer = gl.createBuffer();
   gl.bindBuffer(gl.ARRAY_BUFFER, normalBuffer);
   gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(normals), gl.STATIC_DRAW);
   gl.bindBuffer(gl.ARRAY_BUFFER, null);

   return  {
      position: positionBuffer,
      normal: normalBuffer,
      vertexCount: positions.length/3,
   };
}

Her opprettes et buffer for verteksposisjonene og et buffer for verteksnormalene. Dette tilsvarer det som har vært gjennomgått tidligere.

Kuben defineres vha. to trekanter per side, hver trekant består av 3 vertekser som totalt gir 36 vertekser. Husk at det må være like mange normalvektorer som posisjoner, dvs. 36 normalvektorer.

Verteksposisjonene og verteksnormalverdiene sendes til shaderen via tilsvarende shaderparametre. Det vil si at verteksshaderen, for hver verteks, forventer posisjonsdata og normalvektor. En komplett shader kan f.eks. se slik ut:

<script id="diffuse-vertex-shader" type="x-shader/x-vertex">
    attribute vec3 aVertexPosition;
    attribute vec3 aVertexNormal;    //Normalvektor.

    uniform mat3 uNormalMatrix;    //Transformerer normalvektoren vha. denne.
    uniform mat4 uModelViewMatrix;
    uniform mat4 uProjectionMatrix;

    uniform vec3 uLightDirection;    //Lysets retning.
    uniform vec3 uAmbientLightColor;
    uniform vec3 uDiffuseLightColor;

    varying vec3 vLightWeighting;

    void main() {
        /* Lysbergning... her kommer mer */
        //Transformer vertex:
        gl_Position = uProjectionMatrix * uModelViewMatrix * vec4(aVertexPosition, 1.0);
    }

</script>

Shaderen er ikke komplett, den mangler selve lysberegninga. Som vi ser inneholder den flere lys-relaterte parametre som vil bli brukt til å beregne lys. Dette vil bli forklart etter hvert. Eksempelkoden under viser hvordan vi kopler shaderparametrene til variabler/objekter i Javascriptkoden:

export function main() {
   // Oppretter et webGLCanvas for WebGL-tegning:
   const webGLCanvas = new WebGLCanvas('myCanvas', document.body, 960, 640);
   // Hjelpeobjekt som holder på objekter som trengs for rendring:
   const renderInfo = {
      gl: webGLCanvas.gl,
      baseShader: initBaseShaders(webGLCanvas.gl),
      diffuseLightShader: initDiffuseLightShader(webGLCanvas.gl),

      coordBuffers: initCoordBuffers(webGLCanvas.gl),
      cubeBuffers: initCubeBuffers(webGLCanvas.gl),

      currentlyPressedKeys: [],
      lastTime: 0,
      fpsInfo: {  // Brukes til å beregne og vise FPS (Frames Per Seconds):
         frameCount: 0,
         lastTimeStamp: 0
      },
      light: {
         lightDirection: {x: -10, y:6, z:10},
         diffuseLightColor: {r: 0.1, g: 0.8, b:0.3},
         ambientLightColor: {r: 0.2, g: 0.2, b:0.2},
      },
      animation: {    //Holder på animasjonsinfo:
         angle: 0,
         rotationsSpeed: 60
      }
   };

   const camera = new Camera(renderInfo.gl, renderInfo.currentlyPressedKeys);

   animate( 0, renderInfo, camera);
}

function initDiffuseLightShader(gl) {
   // Leser shaderkode fra HTML-fila: Standard/enkel shader (posisjon og farge):
   let vertexShaderSource = document.getElementById('diffuse-vertex-shader').innerHTML;
   let fragmentShaderSource = document.getElementById('diffuse-fragment-shader').innerHTML;

   // Initialiserer  & kompilerer shader-programmene;
   const glslShader = new WebGLShader(gl, vertexShaderSource, fragmentShaderSource);

   // Samler all shader-info i ET JS-objekt, som returneres.
   return  {
      program: glslShader.shaderProgram,
      attribLocations: {
         vertexPosition: gl.getAttribLocation(glslShader.shaderProgram, 'aVertexPosition'),
         vertexNormal: gl.getAttribLocation(glslShader.shaderProgram, 'aVertexNormal'),
      },
      uniformLocations: {
         projectionMatrix: gl.getUniformLocation(glslShader.shaderProgram, 'uProjectionMatrix'),
         modelViewMatrix: gl.getUniformLocation(glslShader.shaderProgram, 'uModelViewMatrix'),
         normalMatrix: gl.getUniformLocation(glslShader.shaderProgram, 'uNormalMatrix'),

         lightDirection: gl.getUniformLocation(glslShader.shaderProgram, 'uLightDirection'),
         ambientLightColor: gl.getUniformLocation(glslShader.shaderProgram, 'uAmbientLightColor'),
         diffuseLightColor: gl.getUniformLocation(glslShader.shaderProgram, 'uDiffuseLightColor'),
      },
   };
}

I drawCube(), som kalles fra draw(),  sendes lysverdiene inn til shaderen:

function drawCube(renderInfo, camera) {
   // Aktiver shader:
   renderInfo.gl.useProgram(renderInfo.diffuseLightShader.program);

   // Kople posisjon og farge-attributtene til tilhørende buffer:
   connectPositionAttribute(renderInfo.gl, renderInfo.diffuseLightShader, renderInfo.cubeBuffers.position);
   connectNormalAttribute(renderInfo.gl, renderInfo.diffuseLightShader, renderInfo.cubeBuffers.normal);
   connectAmbientUniform(renderInfo.gl, renderInfo.diffuseLightShader, renderInfo.light.ambientLightColor);
   connectDiffuseUniform(renderInfo.gl, renderInfo.diffuseLightShader, renderInfo.light.diffuseLightColor);
   connectLightDirectionUniform(renderInfo.gl, renderInfo.diffuseLightShader, renderInfo.light.lightDirection);

   let modelMatrix = new Matrix4();
   //M=I*T*O*R*S, der O=R*T
   modelMatrix.setIdentity();
   modelMatrix.translate(0,0,0);
   modelMatrix.rotate(renderInfo.animation.angle, 0, 1, 0);
   modelMatrix.scale(0.5,0.5, 0.5);
   camera.set();
   let modelviewMatrix = new Matrix4(camera.viewMatrix.multiply(modelMatrix)); // NB! rekkefølge!
   // Send kameramatrisene til shaderen:
   renderInfo.gl.uniformMatrix4fv(renderInfo.diffuseLightShader.uniformLocations.modelViewMatrix, false, modelviewMatrix.elements);
   renderInfo.gl.uniformMatrix4fv(renderInfo.diffuseLightShader.uniformLocations.projectionMatrix, false, camera.projectionMatrix.elements);

   //Beregner og sender inn matrisa som brukes til å transformere normalvektorene:
   let normalMatrix = mat3.create();
   mat3.normalFromMat4(normalMatrix, modelMatrix.elements);  //NB!!! mat3.normalFromMat4! SE: gl-matrix.js

   renderInfo.gl.uniformMatrix3fv(renderInfo.diffuseLightShader.uniformLocations.normalMatrix, false, normalMatrix);
   renderInfo.gl.drawArrays(renderInfo.gl.TRIANGLES, 0, renderInfo.cubeBuffers.vertexCount);
}

function connectNormalAttribute(gl, shader, normalBuffer) {
   const numComponents = 3;
   const type = gl.FLOAT;
   const normalize = false;
   const stride = 0;
   const offset = 0;
   gl.bindBuffer(gl.ARRAY_BUFFER, normalBuffer);
   gl.vertexAttribPointer(
      shader.attribLocations.vertexNormal,
      numComponents,
      type,
      normalize,
      stride,
      offset);
   gl.enableVertexAttribArray(shader.attribLocations.vertexNormal);
}
function connectAmbientUniform(gl, shader, color) {
   gl.uniform3f(shader.uniformLocations.ambientLightColor, color.r, color.g, color.b);
}
function connectDiffuseUniform(gl, shader, color) {
   gl.uniform3f(shader.uniformLocations.diffuseLightColor, color.r, color.g, color.b);
}
function connectLightDirectionUniform(gl, shader, direction) {
   gl.uniform3f(shader.uniformLocations.lightDirection, direction.x, direction.y, direction.z);
}

Legg merke til normalMatrix - denne har vi ikke brukt før og krever en forklaring. Verteksposisjonene transformeres i verteksshaderen vha. modelview- og projeksjonsmatrisene, som før. Normalvektorene må også transformeres. Normalvektoren representerer en retning og translasjon (forflytning) av denne blir meningsløs. Bruker man modellmatrisa til å transformere normalvektoren og denne inneholder translasjon vil normalvektoren kunne få feil retning. Dersom modellen roterer må normalvektoren rotere tilsvarende. «Uniform» skalering, dvs. lik skalering i alle akser, vil ikke endre normalvektorens retning (kun lengde). «Skeiv» skalering, dvs. ulik skalering i de ulike aksene, vil endre retninga til normalvektoren. Poenget er at man ikke uten videre kan bruke modellmatrisa (eller modelview-matrisa) til å transformere normalvektorene.

For å løse dette bruker vi en egen normalmatrise, som tilsvarer invertert og transponert øvre-venstre 3x3 submatrise av modellmatrisen (evt. modelview-matrisen), til å transformere normalvektorene.

Normalmatrisen genereres typisk i Javascripts-koden og sendes til verteksshaderen som mottar denne via en uniform-variabel (her: uNormalMatrix), på samme måte som den mottar modelview- og projeksjonsmatrisene.

Funksjonen mat3.normalFromMat4() (som ligger i gl-matrix.js biblioteket glMatrix) sørger for å fjerne evt. translasjon (forflytning) som måtte ligge i modellmatrisa. Dette gjøres ved å redusere 4x4 modellmatrise til en 3x3 matrise som tilsvarer øvre venstre 3x3-del av modellmatrisa (translasjon ligger i høyre kolonne i modellmatrisa, som altså fjernes). Denne 3x3 matrisa inverteres og transponeres. Resultatet er en normalmatrise, dvs. en matrise som kan brukes til å transformere normalvektorene.

Retningsorientert lys og diffus refleksjon

Shaderen har nå tilstrekkelig informasjon til å kunne beregne diffus refleksjon når et objekt belyses med retningsorientert lys («sola»), med en gitt retning. 

For å kunne beregne diffus refleksjon trenger vi, som tidligerer nevnt, diffust lys, Id, og diffus materialegenskap, kd. I tillegg må man ta hensyn til lysets retning slik at lysets intensitet avtar med fallende innfallsvinkel – her brukes derfor Lamberts lov:

Diffus refleksjon = kd * Id * max(cosθ, 0)   

Diffus refleksjon tilsvarer da fargen som utgjøres av diffus belysning (Id) og diffus materialegenskap (kd) til objektet som belyses. θ er vinkelen mellom normalvektoren og lysvektoren.

Som indikert i avsnittet om ambient refleksjon er lys og materialegenskapene ofte slått sammen slik at man opererer med en verdi, slik:

            Diffus refleksjon = diffust_lys * max(cosθ, 0)

der diffust_lys f.eks. er lik: [0.1, 0.8, 0.3] (som representerer en nyanse av grønn).

Se kodeeksemplene for demo av diffus refleksjon sammen med retningsorientert lys mot både kube og kule. Her brukes også ambient lys brukes for å heve den generelle belysninga noe. Tilsvarende for punktlys omtales i neste delkapittel.

Komplett shader som brukes til å beregne lys og farge ser slik ut:

<script id="diffuse-vertex-shader" type="x-shader/x-vertex">
    attribute vec3 aVertexPosition;
    attribute vec3 aVertexNormal;    //Normalvektor.

    uniform mat3 uNormalMatrix;    //Transformerer normalvektoren vha. denne.
    uniform mat4 uModelViewMatrix;
    uniform mat4 uProjectionMatrix;

    uniform vec3 uLightDirection;    //Lysets retning.
    uniform vec3 uAmbientLightColor;
    uniform vec3 uDiffuseLightColor;

    varying vec3 vLightWeighting;

    void main() {
        /* Lysbergning:*/
        //Transformer normalvektoren til world-koordinater vha. normalmatrisen:
        vec3 normal = normalize(uNormalMatrix * aVertexNormal);

        //NB! Lysvektoren må normaliseres:
        vec3 lightDirectionNorm = normalize(uLightDirection);
        //Beregn prikkprodukt av lysvektor og normalvektor for diffus belysning:
        float diffusLightWeightning = max(dot(normal, lightDirectionNorm), 0.0);

        //Summer alle refleksjonskomponenter og send til fragmentshader:
        vLightWeighting = uAmbientLightColor + (uDiffuseLightColor * diffusLightWeightning);

        //Transformer vertex:
        gl_Position = uProjectionMatrix * uModelViewMatrix * vec4(aVertexPosition, 1.0);
    }
</script>

Shaderen mottar posisjon og normalvektor for hver verteks – begge av type vec3. Lysberegning utføres dermed per verteks - dvs. i verteksshaderen. Ellers mottas normalmatrisen i tillegg til modelview- og projeksjonsmatrisene (som uniform mat3 og uniform mat4).

Lysberegninga er basert på at lyskilde og normalvektor er i world-koordinater. Det betyr at det forutsettes at lysretning angis (direkte) i forhold til world-koordinatsystemet. Normalvektoren transformeres i shaderen vha. normalmatrisen for å få den i world-koordinater. 

Diffus lysfarge, diffusLightWeightning, for aktuell verteks, beregnes vha. normalisert lysvektor (lightDirectionNorm), transformert normalvektor (normal) og Lamberts lov. Verdien til cosθ i Lamberts lov tilsvarer prikkproduktet mellom normalvektoren og lysvektoren. Resultate tilordnes diffusLightWeightning.

Varying-variabelen vLightWeighting er «komplett» lysfarge for aktuell verteks. Denne er basert på ambient og diffuse lysverdier. vLightWeighting interpoleres på veien til fragmentshaderen der den mottas (også som en varying). OpenGL ES - variabelen gl_Position tilordnes som tidligere forklart.  

Tilhørende fragment-shader ser slik ut:

<script id="diffuse-fragment-shader" type="x-shader/x-fragment">
    precision mediump float;
    varying vec3 vLightWeighting;
    void main() {
        gl_FragColor = vec4(vLightWeighting.rgb, 1.0);
    }
</script>

Her mottas interpolert verdi til vLightWeighting som ble satt i verteksshaderen. Siden dette er en vec3 tilordnes gl_FragColor en vec4-vektor der alpha-verdien settes lik 1.0.

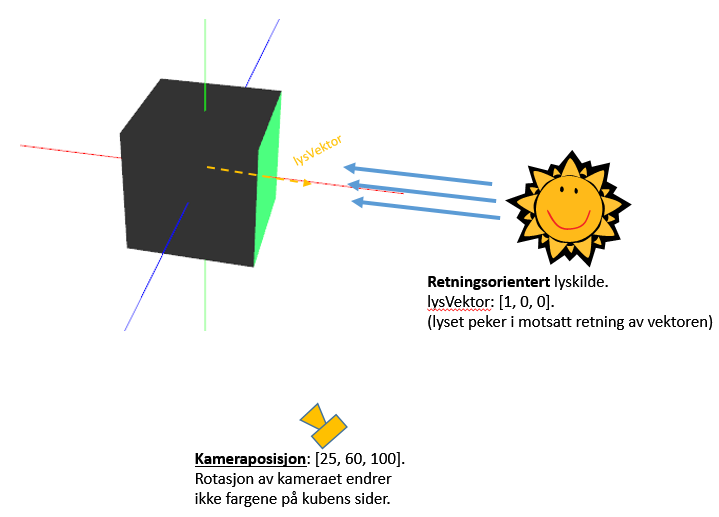
Resultatet blir omtrent som følger når lysvektoren = [1,0,0], dvs. lyset lyser mot negativ x (vektoren oppgis motsatt i forhold til lysretninga). Her er ambient lys = [0.2, 0.2, 0.2] og diffust lys = [0.1, 0.8, 0.3]. Kameraet er plassert i [25, 60, 100]:

Kube belyst med ambient og retningsorientert diffust lys

Som vist i figuren får kuben farge kun på den siden som lyset lyser på. De andre sidene er nesten svart, men er allikevel svakt belyst pga. ambient-lyset. I figuren er posisjon og retning til lyskilden og kameraet indikert (plassering/posisjon er ikke i riktig skala).

I vedlegg 2 kontrolleres det at det vi ser på skjermen stemmer med teorien.

Legg ellers merke til at kubens sider har samme farge uansett hvilken vinkel vi ser kuben fra - fargen er uavhengig av kameraets plassering.

Endring av lysets retning

Dersom vi endrer på lysets retning til [-10, 6.0, 10.0] får vi følgende:

Lysretning: [-10, 6, 10]

Husk at ambient og diffuse-fargene blandes og intensiteten avhenger av lysets innfallsvinkel. Her ser vi tydelig hvordan «shading» utarter seg. Toppen av kuben blir litt mørkere enn fronten siden lysets innfallsvinkel mot toppen er mindre enn mot fronten. Høyre side av kuben er ikke belyst av diffust lys, kun ambient og er derfor nesten helt svart.

Se vedlegg 2 for utregning og kontroll.

Oppgave

Implementer en kule og beregn normalvektorer for kulens trekanter.

Punktlys og diffus refleksjon

Når retningsorientert lys brukes, som gjennomgått i forrige avsnitt, antas det at lyskilden er så langt unna at lysstrålene faller parallelt mot modellen – retningsorientert lys er egentlig et punktlys i uendelig avstand fra modellen.

I dette avsnittet ser vi på punktlys. Dette er en lyskilde som har en posisjon (dvs. i endelig avstand fra modellen). Siden lyskilden har en posisjon må lysvektoren beregnes for hver verteks.

Lysvektoren beregnes ved å ta differansen mellom lyskildens posisjon og verteksposisjonen. Her er det viktig at verteksen og lyskilden er i samme koordinatsystem. I denne gjennomgangen brukes world-systemet, som er enklest og mest naturlig. Verteksen er i «world» koordinatsystemet etter at verteksen er multiplisert med modellmatrisa. Lyskildens posisjon oppgis direkte i world-koordinater. For å kunne beregne lysvektoren i shaderen må modellmatrisa sendes til shaderen (i tillegg til de andre matrisene).

Verteksshaderen ser nå slik ut:

<script id="diffuse-pointlight-vertex-shader" type="x-shader/x-vertex">
    attribute vec3 aVertexPosition;
    attribute vec3 aVertexNormal;  //Normalvektor.

    uniform mat4 uModelMatrix;     //model/world-matrisa brukes til lyskalk.
    uniform mat3 uNormalMatrix;    //Transformerer normalvektoren vha. denne.
    uniform mat4 uModelViewMatrix;
    uniform mat4 uProjectionMatrix;

    uniform vec3 uLightPosition;    //Lysets posisjon.
    uniform vec3 uAmbientLightColor;
    uniform vec3 uDiffuseLightColor;

    varying vec3 vLightWeighting;

    void main() {
        //Transformer verteksposisjon til world-koordinater:
        vec4 vertexPosition = uModelMatrix * vec4(aVertexPosition, 1.0);

        //Beregn vektoren fra denne verteksen til lyskilden:
        vec3 vectorToLightSource = normalize(uLightPosition - vec3(vertexPosition));

        //Transformer normalvektoren til world-koordinater:
        vec3 normal = normalize(uNormalMatrix * aVertexNormal);

        //Beregn prikkprodukt av lysvektor og normalvektor for diffus belysning:
        float diffusLightWeightning = max(dot(normal, vectorToLightSource), 0.0);

        //Summer alle refleksjonskomponenter og send til fragmentshader:
        vLightWeighting = uAmbientLightColor + (uDiffuseLightColor * diffusLightWeightning);

        //Transformer verteksposisjon:
        gl_Position = uProjectionMatrix * uModelViewMatrix * vec4(aVertexPosition, 1.0);
    }
</script>

Verteksposisjonen transformeres vha. modell-matrisa til vektoren vertexPosition. Denne brukes kun til lysberegning.

Lysvektoren, vectorToLightSource, settes lik differansen mellom lyskildens posisjon, uLightPosition, og transformert verteksposisjon. Denne normaliseres også.

Deretter transformeres normalvektoren som videre brukes til å beregne fargen som utgjøres av diffust lys. Verdien legges i diffusLightWeightning.

Variabelen vLightWeighting (og det resterende av shaderkoden) settes på samme måte som i forrige eksempel.  

Dette er illustrert i figuren under:

Lysvektor beregnes per verteks vha. lysposisjon

For at det skal være mulig å beregne lysvektoren må posisjonen til lyskilden sendes inn til verteksshaderen på samme måte som vi sendte inn andre uniform-parametre. I tillegg må modellmatrisa og normalmatrisene sendes til shaderen. Fragmentshaderen tilsvarer også det som ble brukt i forrige eksempel:

<script id="diffuse-pointlight-fragment-shader" type="x-shader/x-fragment">
    precision mediump float;
    varying vec3 vLightWeighting;
    void main() {
        gl_FragColor = vec4(vLightWeighting.rgb, 1.0);
    }
</script>

Oppsummering diffust lys / refleksjon

Vi har nå gjennomgått de to første leddene i likninga:

Totalrefleksjon = ambient refleksjon + diffuse refleksjon + specular refleksjon.

Du finner komplett kode blant kodeeksemplene.

Det siste leddet i likninga omhandler speilrefleksjoner, men først litt mer om ulike typer shading.

Ulike typer shading

Flat shading

En 3D-modell består av mange trekanter. Hver trekant defineres av tre vertekser. For lysberegning må man knytte en normalvektor til hver verteks. Som tidligere forklart kan denne enten være lik trekantens flatenormalvektor eller et gjennomsnitt av tilstøtende trekanters flatenormaler. Når man bruker flatenormaler på hver enklet trekant, i stedet for gjennomsnittsnormalvektorer, kaller vi det flat shading. Dette betyr også at alle fragmentene innenfor trekanten får samme fargeverdi. De små strekene i figuren under illustrerer flatenormalene til hver trekant.

Dersom vi bruker flatenormalene til å gjøre lysberegning vil skillet mellom trekantene vises tydelig som vist i figuren under.

Her ser vi at de ulike trekantene vises tydelig. Her er det benyttet retningsorientert diffust lys (med lilla farge). Jo større trekantene er jo verre blir resultatet. 

Som regel ønsker man i stedet å bruke gjennomsnittsnormalvektoren til å gjøre lysberegninger. Lysberegning kan, uavhengig av hvordan normalvektoren er beregnet, utføres i verteks eller i fragmetshaderen. Dersom vi gjør lysberegning i verteksshaderen kalles det "Gourad shading". Lysberergning i fragmentshaderen kalles "Phong shading". 

Gjennomsnittsnormalvektorer i hver verteks.

Gourad shading

Gourad shading kalles også per-verteks shading siden lysberegninga utføres per verteks og resultatet interpoleres for hvert fragment som inngår i trekanten. Dette betyr at man opererer med (i praksis beregner) normalvektorer for hver enkelt verteks. Det er stort sett denne teknikken vi har benyttet i eksemplene hittil.

Dersom man bruker gjennomsnittsnormalvektoren og Gourad shading til å tegne planet får vi følgende:

Bruk av gjennomsnittsnormalvektorer Gourad shading.

Vi ser nå at skillet mellom trekantene er borte. Generelt vil Gourad shading gi et bra resultat på matte flater.  Skinnende overflater, dvs. bruk av speillys, kan gi ulike «artefakter» siden speillys kun beregnes per verteks. Man kan risikere å miste speillysberegninger som faller mellom verteksene. Bruk av Gourad shading sammen med punktlys kan, i enkelte tilfeller, gi feil belysning. Dette kan unngås ved å bruke Phong shading.

Phong shading

Man kan gjøre all lysberegning per fragment – dette kalles Phong shading (som ikke er det samme som Phong reflection model). Dette kalles også per-fragment-shading.

Dette gir normalt det beste resultatet, spesielt for skinnende overflater. Selv uten bruk av speillys vil Phong shading i mange tilfeller være nødvendig for å få et brukbart resultat. Anta at vi har er punktlys som lyser på en rektangulær flate, bestående av to trekanter.

Punktlys lyser på flate (Anyuru, A., 2012)

I følge det vi har sett på tidligere beregnes diffust lys /intensitet i henhold til følgende formel:

Dette skulle tilsi at lyset i punkt p0 skal være mest intenst (cos0 =1). I verteks v0 og v1 er innfallsvinkelen større som betyr lysets intensitet skal være mindre (cos60=0.5). Dersom Gourad shading brukes i dette tilfellet vil ikke midten av planet bli mest belyst. Her vil lysberegning kun utføres i v0 og v1 og lysfargen ved disse verteksene blir mindre intenst. Fragmentene (dvs. bl.a. p0) mellom disse verteksene får interpolerte verdier og vil også fremstå med svakere intensitet. Resultatet blir derfor ikke tilfredsstillende i dette tilfellet.

Dersom Phong shading benyttes sendes normalvektoren knyttet til hver verteks videre til fragmentshaderen slik at all lysberegning i stedet kan gjøres her – dvs. per fragment. Normalvektoren sendes som en varying til fragmentshaderen slik at fragmentshaderen mottar en (lineær) interpolert normalvektor.

I forhold til eksemplet med en belyst flate vil det nå utføres en egen lysberegning i p0 slik at dette punktet får korrekt belysning (dvs. mest intenst lys).

Phong shading er den mest GPU-krevende teknikken siden beregninger utføres per fragment i stedet for per verteks.

Det kan i enkelte tilfeller være vanskelig å se forskjell på bruk av Gourad og Phong-shading.

Blande lys, verteksfarge & tekstur

Blande verteksfarge og lys

Dersom man knytter farge til verteksene vil fargen interpoleres over trekantenes fragmenter. Vi har også sett at vi kan gi modeller farge ved hjelp av diverse lysparametre. Det er også mulig å blande verteksfarger med lys.

Verteksshaderen må da, i tillegg til posisjon og normalvektor, også ta i mot verteksfarge og blandes med lysfargen. Fragmentshaderen endres som følger:

. . .
varying vec3 vColor;
. . .
void main() {
    . . .

    gl_FragColor = vec4(lightWeighting.rgb * vColor.rgb, 1.0);
}

Her vil beregnet lysfarge (lightWighting) blandes med interpolert verteksfarge (vColor).

Blande teksturer og lys

Teksturering av 3D-modeller er med på å øke 3D realismen. Det samme gjelder belysning og spesielt med bruk av speilbelysning. Dersom vi nå blander disse elementene, dvs. at vi belyser en teksturert modell vil 3D effekten kunne bli enda bedre.

Dette er egentlig ganske enkelt. Lysberegning gjøres som vist i eksemplene over. I fragmentshaderen blandes lysfarge og teksturfarge som vist under:

. . .

varying lowp vec2 vTextureCoordinate;

uniform sampler2D uSampler;

void main() {

  . . .

  //Summer alle refleksjonskomponenter og send til fragmentshader:

  vec3 lightWeighting = uAmbientLightColor + (uDiffuseLightColor * diffusLightWeightning);

  gl_FragColor = vec4(lightWeighting.rgb, 1.0) + texture2D(uSampler, vec2(vTextureCoordinate.s, vTextureCoordinate.t));

}

Variabelen vTextureCoordinate representerer teksturkoordinat for aktuelt fragment og er en interpolert verdi. Fargeverdien til dette fragmentet hentes («samples») fra teksturen vha. texture2D() funksjonen. Denne blandes så med lysfargen og gir endelig farge som tilordnes gl_FragColor.

Noen tips i forhold til Blender og eksport (threejs)

Vha. Blender lager man enkelt en kule (bruk Add | Mesh | UV Sphere i Blender) som eksporteres til et eller annet format, f.eks. obj, fbx e.l. Eksportert fil må deretter importeres i vårt program slik at verteks- og normalvektorbuffer kan fylles med data. NB! Å skrive en slik "importer" selv er en krevende øvelse. Det anbefales derfor å bruke three.js som allerede har slike importere og som derfor gjør denne prosessen relativt enkel. Dette avsnittet er derfor ikke så aktuelt så lenge man kun bruker ren WebGL.

Før eksport fra Blender må man passe på å «triangulere» kula slik at alle «Faces» består av trekanter i stedet for firkanter (trykk Ctrl+T i Edit Mode). I Blender kan man visualisere normalvektorene til kula ved å trykke på "Show Overlays" i edit mode, og velge Normals. 

Her kan man velge å se enten flatenormalene, verteksnormalene eller begge deler. I figuren over vises flatenormalene mens figuren under viser verteksnormalene:

Normalvektorer illustrert i Blender

Ved eksport fra Blender krysser vi av for «Normals» som vist under:

Kulemodellen kan nå importeres i threejs - programmet slik at verteks- og normalvektorbuffer fylles med data.