WebGL og grunnleggende 3D transformasjoner
Dette avsnittet beskriver hvordan transformasjonsmatrisene brukes til å gjengi (rendre) 3D-geometri i form av primitiver/trekanter, som settes sammen til objekter/modeller, på en 2D skjerm.3D modellene består av et sett primitiver som igjen består av et sett vertekser. En verteks tilsvarer et punkt i rommet, spesifisert vha. koordinatverdiene x, y og z. I tillegg kan man assosiere en farge, teksturkoordinat og normalvektor til en verteks – en verteks kan med andre ord inneholde mer enn bare koordinatverdiene x, y, z.
Man kan tegne primitiver/trekanter direkte på «canvaset» ved å bruke såkalte normaliserte koordinatverdier, dvs. verdiene til x,y og z i området [-1, 1]. Disse verdiene er uavhengig av skjerm/canvas-størrelse og er egentlig koordinatsystemet som OpenGL ES forholder seg til.
 |
| Fra NDC til skjermkoordinater |
Dette koordinatsystemet vil deretter avbildes («mappes») til canvaset, som tilsvarer det vi kaller «viewport». Normalt vil hele canvaset, dvs. det grønne området i figuren over, tilsvare viewporten.
Når trekanten i figuren over har koordinatverdier i dette området vil den vises på skjermen/canvaset som vist til høyre i figuren. Merk at figuren inkluderer koordinataksene – disse må evt. tegnes vha. egne linjer om de skal vises.
Videre skal vi se hvordan vi kan definere 3D-modeller med vilkårlige koordinatverdier. Vi vil se hvordan modeller defineres i sitt eget, lokale, koordinatsystem og deretter «plasseres» i det «globale koordinatsystemet». Ved hjelp at ulike transformasjoner, kamera og projeksjon vil modellens koordinater til slutt ende opp med normaliserte koordinatverdier som kan gjengis på skjermen med 3D-effekt.
Vi ønsker f.eks. å kunne bruke koordinatverdier som illustrert i figuren under og allikevel få den frem på skjermen som vist under:
 |
| Bruk av vilkårlige koordinatverdier |
Her er trekanten definert av verteksene [-10, -10, 0], [10, -10, 0] og [0, 10, 0]. Koordinatverdiene transformeres (T) deretter slik at de kan fremstilles på skjermen som en trekant som vist til høyre i figuren. Legg merke til at vi ser trekanten i perspektiv – dette vil også bli forklart her.
Her ser vi at negativ z går «innover» i skjermen mens positiv z går utover. «Øyet» i figuren representerer det «virtuelle» kamera som er med på å bestemme hva som vises på skjermen. Dette peker i utgangspunktet mot negativ z.
Verteksshaderen vil normalt transformere hver verteks vha. diverse 4x4 matriser, normalt en såkalt modelview-matrise og en projeksjons-matrise. Disse sendes normalt til verteksshaderen slik at de er tilgjengelig når verteksshaderen transformerer verteksene. Disse matrisene vil bli omtalt mer etter hvert.
Videre skal vi se på et eksempel som tegner en enkel trekant med koordinatverdier (x, y, z) i området -2.5 - +2.5 som transformeres og projiseres slik at den til slutt vises på skjermen.
Tilhørende Javascript-kode:
Posisjnonsbufret opprettes ved hjelp av tre posisjoner siden det er en enkel trekant som skal tegnes – se initBuffers() metoden. Disse har koordinatverdiene:
Modellmatrisa gjør, i dette tilfellet, ingenting siden den er satt lik identitetsmatrisa. View-matrisa sørger for å plassere kameraet i [0,0,100] orientert mot origo. Kamera må peke mot modellen for at den skal vises på skjermen. Disse to matrisene slås sammen til en modelview-matrise. Her er det viktig at matrisene multipliseres i korrekt rekkefølge. Kodelinja
Projektsjonsmatrisa er med på å begrense hvilken del av 3D-verden som skal vises på skjermen samt å sørge for at alle verteksene omgjøres til såkalte «clip-koordinater». Disse matriseoperasjonene vil bli forklart nærmere i neste avsnitt.
I verteksshaderen er følgende parametre definert:
Videre ser vi at den innebygde variabelen gl_Position settes lik aVertexPosition multiplisert med de to nevnte matrisene (NB! Må gjøres i korrekt rekkefølge, mer etter hvert).
Legg også merke til at aVertexPosition gjøres om slik at homogene koordinater benyttes. Dette gjøres vha. vec4(aVertexPosition, 1) slik at den «homogene verteksen» blir (x,y,z,1). Se eget notat om vektorer og matriser som forklarer mer om homogene koordinater.
Variabelen gl_Position er en GLSL spesifikk variabel. Hovedoppgaven til verteksshaderen er å gi denne variabelen en verdi. Som regel settes denn lik produktet av verteksen, modellview- og projeksjonsmatrisene. Verteksen sine koordinater (x,y,z,w) er nå gjort om til såkalte "clip-koordinater". Se figur under.
I tillegg utføres (automatisk, vi trenger egentlig ikke tenke på dette):
Både viewport-transformasjonen og «perspective division» utføres (automatisk) i steget etter verteksshaderen, dvs. i steget "Sammenstilling av primitiver".
Vi ser dette i figuren under, som er et utsnitt av tidligere vist graphics pipeline.
Verteksshanderen utfører vertekstransformasjonen ved å multiplisere verteksen med både modelview- og projeksjonsmatrisa. Dette betyr at shaderen må ha tilgang på disse matrisene. Normalt leveres disse fra «klientprogrammet» (WebGL/Javascript) før verteksene sendes til shaderen.
Etter at verteksen er multiplisert med modelview-matrisa sier vi at verteksene er transformert til «øye-koordinater». Hvorfor det kalles «øye-koordinater» vil bli tydeligere når vi ser mer på view-transformasjon.
Den transformerte verteksen multipliseres så med projeksjonsmatrisa og er da transformert til «clip-koordinater». Den transformerte verteksen tilordnes til slutt i verteksshaderen til gl_Position.
Verteksen er nå omgjort til såkalte NDC (Normalized Device Coordinates). Det vil si at alle vertekser som har koordinatverdier (x, y og z) i området [-1, 1] vil være med videre i pipelinen. Vertekser med koordinater utenfor dette området vil «clippes» vekk – de er ikke med videre. Primitiver som er delvis innenfor deles i to. Tenk på dette som om frustumet strekker seg fra -1 til +1 i x,y og z-retning.
Deretter utføres «viewport»-transformasjonen (dette gjøres ikke ved hjelp av en matrise), dvs. at NDC mappes til det området på skjermen som skal vise resultatet.
Se også (OpenGL Wiki, Vertex Transformation, 2012) og her for mer info.
Modellen(e) (trekanten(e)) er nå brutt ned til et sett fragmenter. Et fragment er en «kandidat» til å bli en piksel i skjermbufret, ikke alle fragmenter ender opp som piksler i skjermbufret. Hvert fragment sendes nå til fragmenthaderen (kalles pikselshader i Direct3D-terminologi).
Fragmentshaderen vil typisk motta en farge som et parameter. I sin enkleste for vil fragmentshaderen kun videresende denne ved å sette gl_FragColor lik parameterverdien. Alternativt kan den f.eks. gjøre ulike lysberegninger som påvirker endelig farge på fragmentet. Uansett må fragmentshaderen sette gl_FragColor lik en verdi.
I kodeeksemplet over får alle pikslene samme farge via fragmentshader-parametret u_FragColor. Dette er også en «uniform» og har samme verdi for alle piksler. Verdien til denne sendes fra bindShaderParameters() metoden i WebGL/Javascrips-koden.
Alternativ kunne man knyttet en farge til hver verteks og brukt disse til å gi farge til pikslene til trekanten. Fargen knyttet til verteksene ville i så fall bli «interpolert» (utjevnet) over trekantenes flater.
Fragmentene går via flere steg før de ender opp i skjermbufret (framebuffer). Mer om dette senere.
På tilsvarende måte konstrueres 3D modeller i WebGL. Modellene defineres i forhold til et tenkt lokalt koordinatsystem (model space) og gjerne sentrert rundt origo. Deretter "plasseres modellen" i det "globale" koordinatsystemet (world space) ved hjelp av en koordinattransformasjon / matrisemultiplikasjon. Se (Luna, 2006), (Angel E. & David S., 2015) og (Matsuda et.al, 2013, vedlegg G).
Når vi i Javascript-koden spesifiserer en modell, f.eks. en kube, oppgir vi verteksene i et tenkt lokalt koordinatsystem. Verteksene sine koordinater kalles da modellkoordinater (se tidligere figur). Vha. en modelltransformasjon kan vi posisjonere og orientere kuben i det globale koordinatsystemet (world space).
Hver enkelt modell kan har sin egen modelltransformasjon. Når alle modellene er transformert inn i det globale koordinatsystemet er alle i samme koordinatsystem. En modelltransformasjon består normalt av en eller flere av følgende i kombinasjon:
Dersom man f.eks. definerer et hus spesifiserer man alle verteksene i modellkoordinater for deretter å gjøre nødvendige transformasjoner. Dette kan f.eks. bety å skalere huset opp eller ned, rotere og evt. flytte det dit man måtte ønske i forhold til det globale systemet. Se figuren under.
Den sammensatte transformasjonen representeres av en 4x4 matrise som multipliseres med alle verteksene.
Legg merke til at dersom man setter modellmatrisa lik identitetsmatrisa vil modellen «plasseres direkte» i det globale systemet.
Dette betyr at dersom man ikke angir en modellmatrise, eller den settes lik identitetsmatrisa, utføres ingen rotasjon, skalering eller translering av opprinnelig modell.
Det finnes egentlig ikke noe kameraobjekt i WebGL/OpenGL ES. Vi tenker oss i stedet at vi plasserer et kamera et sted i det globale koordinatsystemet og orienterer det mot objektene/modellene som vi ønsker skal vises på skjermen. Se figur.
Vha. view-transformasjonen kan vi posisjonere og orientere dette «virtuelle» kameraet der vi måtte ønske. I utgangspunktet, dvs. dersom view-matrisa = identitetsmatrisa, står kameraet i origo og ser langs negativ z-akse. Dette betyr at kameraet i utgangspunktet ikke nødvendigvis vil se alle modeller/figurer. For at kameraet skal se modeller som er bak eller ved siden av kameraet må enten modellene flyttes foran kameraet eller så må kameraet flyttes og roteres slik at det ser modellene.
Ved hjelp av view-matrisa transformeres verteksene til modellen(e) motsatt i forhold til hvor du ønsker å flytte kamera (man kan tenke seg at kameraet står i origo og at modellene flyttes i forhold til dette).
Dersom man tenker seg at kameraet skal flyttes +5 enheter langs z-aksen vil det vær det samme som om vi flyttet modellen(e) -5 enheter langs z-aksen. Modell- og view-transformasjonene er egentlig to sider av samme sak. Dette vil bli nærmere forklart i avsnittet om modelview-transformasjonen.
View-transformasjonen består egentlig av en kombinasjon av en translasjon og en rotasjon.
Etter view-transformasjonen er koordinatene transformert til øyekoordinater (og modellen er i «view space»).
Ved hjelp av funksjonen mat4.lookAt(parametre) kan man generere en View-matrise. Parametrene til denne funksjonen omfatter bl.a. kameraets posisjon og punktet det peker/ser mot.
Bruk av glMatrix-biblioteket (bruker også vec3-klassen):
let v3Eye = vec3.fromValues(7.0, 6.0, 16.0); //Eksempler
let v3Look = vec3.fromValues(0.0, 0.0, 0.0);
let v3Up = vec3.fromValues(0.0, 1.0, 0.0);
let viewMatrix = mat4.create();
mat4.lookAt(viewMatrix, v3Eye, v3Look , v3Up);
Bruk av cuon-matrix.js (Matsuda et.al, 2013) biblioteket:
let viewMatrix = new Matrix4();
viewMatrix.setLookAt(eyeX, eyeY, eyeZ, lookX, lookY, lookZ,
upX, upY, upZ);
Eye-koordinatene tilsvarer kameraets posisjon. Look- koordinatene tilsvarer punktet kameraet peker mot og Up- koordinatene definerer hva som er opp/ned på kameraet (som regel upX=0, upY=1, upZ=0).
Når man spesifiserer viewmatrisa er det selvfølgelig viktig at kameraet peker mot modellen(e), hvis ikke vil den ikke vises på skjermen. Som vi straks skal se vil også projeksjonsmatrisa være med på avgrense hva som ender opp på skjermen.
Enten flytter man modellen i den ene retninga eller så flytter man kameraet i motsatt retning.

Begrepet «modelview» betyr at modell- og viewtransformasjonsmatrisene slås sammen til en matrise.
I enkelte tilfeller kan det være praktisk å håndtere disse som to separate matriser men de må uansett slås sammen for å få utført korrekt transformasjoner på verteksene. I praksis vil man ofte slå sammen disse to matrisene i Javascript-koden og sende resultatmatrisa (altså «modelview-matrisa») til verteksshaderen. Alternativt kan begge sendes inn til shaderen som da får ansvaret for å multiplisere disse sammen.
I tidligere versjoner av både standard OpenGL og ES-versjonen var det ikke støtte for programmerbare shadere («fixed function pipeline») og her opererte man kun med modelview-matrisa.
En vanlig analogi innen 3D grafikk er å sammenlikne modell-, view- og projeksjonstransformasjonene med det å ta et bilde med et kamera. Modelltransformasjonen tilsvarer det å plassere modellene i scenen. View-transformasjonen tilsvarer å plassere og orientere kameraet mot modellene(e) mens projeksjonstransformasjonen tilsvarer det å velge en linse til kameraet. Kameralinsa påvirker hva kameraet ser og til en viss grad hvordan modellene vil se ut.
Det finnes to typer projeksjoner:
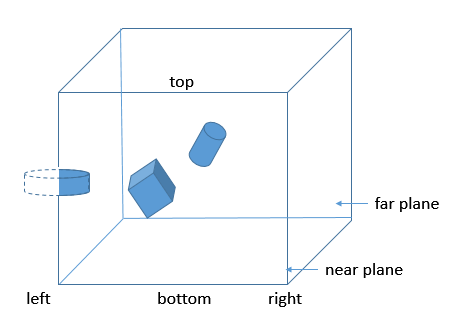
Når ortografisk projeksjon brukes vil «view-volumet» være en rektangulær boks. Primitiver (trekanter) som faller innenfor volumet vil projiseres på «near-plane» (se figur under) og vises i den endelige scenen. Primitiver som er delvis innenfor vil «klippes»/deles opp. Resten vil ikke vises, dvs. verteksene til primitiver som faller utenfor blir ikke sendt videre i «pipelinen».
Man kan f.eks. bruke mat4.ortho(…) funksjonen, definert i glMatrix, til å generere en ortografisk matrise:
View-volumet som genereres ved perspektivprojeksjon kalles et frustum som ser ut som en avkappet pyramide.
Vertekser (og dermed primitiver og objekter) som ligger helt eller delvis innenfor denne pyramiden representerer det som kameraet ser. Denne transformasjonen sørger dermed for to ting:
Det er to typer funksjoner man kan bruke til å generere en projeksjonsmatrise:
glMatrix-biblioteket:
let projectionMatrix = mat4.create();
mat4.perspective(fovy, aspect, near, far, projectionMatrix);
cuon-matrix.js:
let projectionMatrix = new Matrix4();
projectionMatrix.setPerspective(fovy, aspect, near, far);
Parametrene er som følger:
 Matrisa kan beregnes slik:
Matrisa kan beregnes slik:
Det kan nevnes at moderne grafikkort automatisk ”culler” det som faller utenfor frustumet. Men, og dette er viktig, det betyr ikke at WebGL-programmet automatisk vet hvilke objekter som ligger innafor frustumet og hvilke som ligger utenfor (dette bestemmes jo av View og projeksjonsmatrisene). Dette betyr igjen at dersom vi har en stor scene med mange objekter som skal tegnes og kameraet peker en vei vil tegnekommandoen (drawArrays()) bli utført for alle objekter uansett om de ligger innafor eller utenfor frustumet. Grafikkortet/pipelinen vil imidlertid sørge for å fjerne objekter som faller utenfor.
. . .
// Definerer modellmatrisa (rotasjon + translasjon):
modelMatrix.setTranslate(-20, 10, 0);
modelMatrix.rotate(45, 0, 0, 1);
. . .
Dette gjør at modellen først roterer 45 grader om egen akse for deretter å flytte -30 langs x-aksen. Her settes, vha. setTranslate(), modellmatrisa først lik en translasonsmatrise. Denne multipliseres så med en rotasjonsmatrisa ved hjelp av rotate() metoden. Metoder som starter med set, f.eks. setTranslate(), nullstiller og oppretter en ny matrise som kun inneholder en translasjon. Metoder uten set, som rotate(), endrer (her) modelMatrix ved å multiplisere med en rotasjonsmatrise.
Selv om pikselfargene er beregnet og returnert fra fragmentshaderen kan fragmentet fortsatt bli forkastet pga. ulike tester som utføres i dette steget.
Scissor test:
Man kan sette et såkalt ScissorRectangle for å begrense tegning til en mindre del av skjermen/vinduet. Settes på GraphicsDevice-objektet.
Stencil test:
Bruker et spesielt buffer, et stencil buffer, og brukes i spesielle tilfeller til avanserte rendringteknikker.
Depth test:
Ved hjelp av verteksene beregnes også dybdeinformasjon til hver enkelt fragment – hver enkelt fragment har tilknyttet dybdeinformasjon. Dette lagres i et eget buffer som kalles z-buffer eller bare dybde(depth) buffer. Dette er med på å avgjøre hvilke modeller som ligger fremst i bildet og dermed skal vises og hvilke som ikke skal med i det endelige bildet.
Alpha blending:
Dersom alpha blending benyttes vil fragmentets farge blandes med fargen til andre fragmenter (som ligger over eller under).
Vi tar utgangspunkt i følgende figur for å definere nødvendige vertekser:

Her ser vi kuben og verteksposisjonene til kubens hjørner. Det er også antydet at hver siden av kuben består av to trekanter. I tillegg er koordinataksene vist. Dersom kuben tegnes vha. drawArrays(gl.TRIANGLES, …) kan følgende verteksposisjonsarray benyttes:
Bruker vi indekser til å tegne kuben holder det å angi 8 vertekser i tillegg til 36 indekser.
Koordinatsystemer
I WebGL defineres verteksene til figurer/modeller i forhold til et høyrehånds koordinatsystem. Figuren under viser dette i forhold til «skjermen».| Koordinatsystemet til WebGL (Matsuda et.al., 2013) |
Steg for å lage et WebGL program
Kort oppsummert vil et typisk WebGL/Javascript program gjøre følgende for å få tegnet en 3D-modell:- Definere verteksene til modellen i et tenkt lokalt koordinatsystem. Det er som regel fordelaktig å sentrere modellen om origo.
- Lage en modellmatrise som inneholder en, eller en kombinasjon, av følgende transformasjoner: translasjon, rotasjon og skalering. Vha. modellmatrisa "plasseres" modellen i det globale koordinatsystemet.
- Lage en viewmatrise som spesifiserer hvilken del av «scenen» som skal vises på skjermen. Man tenker seg at man plasserer et kamera i det globale systemet. Det som kameraet «ser» er det som ender opp på skjermen.
- Lage en projeksjonsmatrise. Denne bestemmer hvordan 3D-verden/scenen skal projiseres på skjermen. I tillegg er den med på å avgrense hva som vises.
- Multiplisere sammen modell- og viewmatrisene til en modelview-matrise.
- Sende modelview-matrisa og projeksjonsmatrisa til verteksshaderen.
- Verteksshaderen bruker disse til å transformere hver enkelt verteks. Resten av «jobben», deriblant sammenstilling av primitiver/trekanter, rasterisering m.m. utføres av GPU’en og fragmentshaderen.
Mer om graphics pipeline
Open GL ES sin «graphics pipeline» viser hvilke steg som inngår for å få definerte modeller og primitiver til å vises på skjermen. Den viser også hvilke transformasjoner som utføres fra verteksene leveres fra WebGL/Javascript-programmet til det endelige bildet kan vises på skjermen.| Figuren er basert på tilsvarende fra (Munshi et.al., 2009) |
Shader
Når vi bruker OpenGL ES & WebGL er vi nødt til å forholde oss til shadere. Shadere er programmer, skrevet i sitt eget språk - GLSL, som kjører direkte på maskinens GPU. Man legger som regel shaderkoden som en del av WebGL/Javascript-koden.Verteksshaderen vil normalt transformere hver verteks vha. diverse 4x4 matriser, normalt en såkalt modelview-matrise og en projeksjons-matrise. Disse sendes normalt til verteksshaderen slik at de er tilgjengelig når verteksshaderen transformerer verteksene. Disse matrisene vil bli omtalt mer etter hvert.
Videre skal vi se på et eksempel som tegner en enkel trekant med koordinatverdier (x, y, z) i området -2.5 - +2.5 som transformeres og projiseres slik at den til slutt vises på skjermen.
Kodeeksempel
Vi tar utgangspunkt i et kodeeksempel som tegner en enkel trekant. Verteksene legges i et verteksbuffer. Legg merke til koordinatverdiene til de tre verteksene som utgjør trekanten – disse ligger i området [-2.5, 2.5]. Vi ser først på html-fila:<!DOCTYPE html>
<html lang="nb">
<head>
<meta charset="utf-8">
<title>WebGL Hello Triangle</title>
<link rel="stylesheet" href="../../base/webgl.css" type="text/css">
<script src="../../base/lib/cuon-matrix.js"></script>
<script src="../../base/lib/gl-matrix.js"></script>
</head>
<body>
<div style="top:0px; left:15px; width:100%; text-align:left; color:black;" class="ui">
<h2>WebGL Hello Triangle</h2>
</div>
<!-- SHADERS -->
<script id="base-vertex-shader" type="x-shader/x-vertex">
attribute vec3 aVertexPosition;
attribute vec4 aVertexColor;
uniform mat4 uModelViewMatrix;
uniform mat4 uProjectionMatrix;
varying lowp vec4 vColor;
void main(void) {
gl_Position = uProjectionMatrix * uModelViewMatrix * vec4(aVertexPosition, 1.0);
vColor = aVertexColor;
gl_PointSize = 10.0; //Merk: Kun i bruk når man tegner POINTS
}
</script>
<script id="base-fragment-shader" type="x-shader/x-fragment">
varying lowp vec4 vColor;
void main(void) {
gl_FragColor = vColor;
}
</script>
<script type="module" >
'use strict';
import {main} from "./helloTriangle.js";
main();
</script>
</body>
</html>
Tilhørende Javascript-kode:
'use strict';
/**
* The purpose of "use strict" is to indicate that the code should be executed in "strict mode".
* With strict mode, you can not, for example, use undeclared variables.
* https://www.w3schools.com/js/js_strict.asp
*/
import {WebGLCanvas} from '../../base/helpers/WebGLCanvas.js';
import {WebGLShader} from '../../base/helpers/WebGLShader.js';
/**
* Et WebGL-program som tegner en enkel trekant.
* Bruker ikke klasser, kun funksjoner.
*/
export function main() {
// Oppretter WebGL-kontekst for 3D/WebGL-tegning:
const canvas = new WebGLCanvas('myCanvas', document.body, 960, 640);
const gl = canvas.gl;
let shaderInfo = initShaders(gl);
let cameraMatrixes = initCamera(gl);
let buffers = initBuffers(gl);
draw(gl, shaderInfo, buffers, cameraMatrixes);
}
function initShaders(gl) {
// Leser shaderkode fra HTML-fila: Standard/enkel shader (posisjon og farge):
let vertexShaderSource = document.getElementById('base-vertex-shader').innerHTML;
let fragmentShaderSource = document.getElementById('base-fragment-shader').innerHTML;
// Initialiserer & kompilerer shader-programmene;
const glslShader = new WebGLShader(gl, vertexShaderSource, fragmentShaderSource);
// Samler all shader-info i ET JS-objekt, som returneres.
return {
program: glslShader.shaderProgram,
attribLocations: {
vertexPosition: gl.getAttribLocation(glslShader.shaderProgram, 'aVertexPosition'),
vertexColor: gl.getAttribLocation(glslShader.shaderProgram, 'aVertexColor'),
},
uniformLocations: {
projectionMatrix: gl.getUniformLocation(glslShader.shaderProgram, 'uProjectionMatrix'),
modelViewMatrix: gl.getUniformLocation(glslShader.shaderProgram, 'uModelViewMatrix'),
},
};
}
/**
* Genererer view- og projeksjonsmatrisene.
* Disse utgjør tilsanmmen det virtuelle kameraet.
*/
function initCamera(gl) {
// Kameraposisjon:
const camPosX = 0;
const camPosY = 0;
const camPosZ = 10;
// Kamera ser mot ...
const lookAtX = 0;
const lookAtY = 0;
const lookAtZ = 0;
// Kameraorientering:
const upX = 0;
const upY = 1;
const upZ = 0;
let viewMatrix = new Matrix4();
let projectionMatrix = new Matrix4();
// VIEW-matrisa:
viewMatrix.setLookAt(camPosX, camPosY, camPosZ, lookAtX, lookAtY, lookAtZ, upX, upY, upZ);
// PROJECTION-matrisa (frustum): cuon-utils: Matrix4.prototype.setPerspective = function(fovy, aspect, near, far)
const fieldOfView = 45; // I grader.
const aspect = gl.canvas.clientWidth / gl.canvas.clientHeight;
const near = 0.1;
const far = 1000.0;
// PROJEKSJONS-matrisa; Bruker cuon-utils: Matrix4.prototype.setPerspective = function(fovy, aspect, near, far)
projectionMatrix.setPerspective(fieldOfView, aspect, near, far);
return {
viewMatrix: viewMatrix,
projectionMatrix: projectionMatrix
};
}
/**
* Oppretter verteksbuffer for trekanten.
* Et posisjonsbuffer og et fargebuffer.
* MERK: Må være likt antall posisjoner og farger.
*/
function initBuffers(gl) {
const width = 5;
const height = 5;
const positions = new Float32Array([
0.0, height/2, 0.0, // X Y Z
-width/2, -height/2, 0.0, // X Y Z
width/2, -height/2, 0.0 // X Y Z
]);
const colors = new Float32Array([
1, 0.3, 0, 1, //R G B A
1, 0.3, 0, 1, //R G B A
1, 0.3, 0, 1, //R G B A
]);
const positionBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, positionBuffer);
gl.bufferData(gl.ARRAY_BUFFER, positions, gl.STATIC_DRAW);
gl.bindBuffer(gl.ARRAY_BUFFER, null);
const colorBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, colorBuffer);
gl.bufferData(gl.ARRAY_BUFFER, colors, gl.STATIC_DRAW);
gl.bindBuffer(gl.ARRAY_BUFFER, null);
return {
position: positionBuffer,
color: colorBuffer,
vertexCount: positions.length/3
};
}
/**
* Aktiverer position-bufferet.
* Kalles fra draw()
*/
function connectPositionAttribute(gl, shaderInfo, positionBuffer) {
const numComponents = 3;
const type = gl.FLOAT;
const normalize = false;
const stride = 0;
const offset = 0;
gl.bindBuffer(gl.ARRAY_BUFFER, positionBuffer);
gl.vertexAttribPointer(
shaderInfo.attribLocations.vertexPosition,
numComponents,
type,
normalize,
stride,
offset);
gl.enableVertexAttribArray(shaderInfo.attribLocations.vertexPosition);
}
/**
* Aktiverer color-bufferet.
* Kalles fra draw()
*/
function connectColorAttribute(gl, shaderInfo, colorBuffer) {
const numComponents = 4;
const type = gl.FLOAT;
const normalize = false;
const stride = 0;
const offset = 0;
gl.bindBuffer(gl.ARRAY_BUFFER, colorBuffer);
gl.vertexAttribPointer(
shaderInfo.attribLocations.vertexColor,
numComponents,
type,
normalize,
stride,
offset);
gl.enableVertexAttribArray(shaderInfo.attribLocations.vertexColor);
}
/**
* Klargjør canvaset.
* Kalles fra draw()
*/
function clearCanvas(gl) {
gl.clearColor(0.9, 0.9, 0.9, 1); // Clear screen farge.
gl.clearDepth(1.0);
gl.enable(gl.DEPTH_TEST); // Enable "depth testing".
gl.depthFunc(gl.LEQUAL); // Nære objekter dekker fjerne objekter.
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
}
/**
* Tegner!
*/
function draw(gl, shaderInfo, buffers, cameraMatrixes) {
clearCanvas(gl);
// Aktiver shader:
gl.useProgram(shaderInfo.program);
// Kople posisjon og farge-attributtene til tilhørende buffer:
connectPositionAttribute(gl, shaderInfo, buffers.position);
connectColorAttribute(gl, shaderInfo, buffers.color);
// Lag viewmodel-matris::
let modelMatrix = new Matrix4();
modelMatrix.setIdentity();
let modelviewMatrix = new Matrix4(cameraMatrixes.viewMatrix.multiply(modelMatrix)); // NB! rekkefølge!
// Send matrisene til shaderen:
gl.uniformMatrix4fv(shaderInfo.uniformLocations.modelViewMatrix, false, modelviewMatrix.elements);
gl.uniformMatrix4fv(shaderInfo.uniformLocations.projectionMatrix, false, cameraMatrixes.projectionMatrix.elements);
// Tegn!
gl.drawArrays(gl.TRIANGLES, 0, buffers.vertexCount);
}
Programmet bruker et position og et color-array og buffer til å tegne en enkel trekant på canvaset eller «viewporten». «Viewporten» tilsvarer den delen av skjermen, html5-canvaset i dette tilfellet, som den endelige tegninga vises på.
Posisjnonsbufret opprettes ved hjelp av tre posisjoner siden det er en enkel trekant som skal tegnes – se initBuffers() metoden. Disse har koordinatverdiene:
const positions = new Float32Array([
0.0, height/2, 0.0, // X Y Z
-width/2, -height/2, 0.0, // X Y Z
width/2, -height/2, 0.0 // X Y Z
]);
Fargebufret
Vi bruker et eget buffer for fargene. Merk at det må være like mange farger som posisjoner. Hver verteks består dermed av en posisjon og en farge. Fargebufret opprettes vha. følgende array:
const colors = new Float32Array([
1, 0.3, 0, 1, //R G B A
1, 0.3, 0, 1, //R G B A
1, 0.3, 0, 1, //R G B A
]);
Disse tre verteksene (posisjon+farge) vil bli sendt, en og en, til verteksshaderen etter at drawArrays() er utført, se draw() metoden. I draw() koples posisjon- og fargeattributtene til tilsvarende buffer. Deretter generes modelview matrisa vha. view og projeksjonsmatrisene. Disse ble initiert i initCamera() og er tilgjengelig via cameraMatrixes. Viewmodel og projeksjonsmatrisene sendes så til verteksshaderen før vi kaller på drawArrays().
Modellmatrisa gjør, i dette tilfellet, ingenting siden den er satt lik identitetsmatrisa. View-matrisa sørger for å plassere kameraet i [0,0,100] orientert mot origo. Kamera må peke mot modellen for at den skal vises på skjermen. Disse to matrisene slås sammen til en modelview-matrise. Her er det viktig at matrisene multipliseres i korrekt rekkefølge. Kodelinja
- modelviewMatrix = viewMatrix.multiply(modelMatrix);
- modelviewMatrix = viewMatrix * modelMatrix
Projektsjonsmatrisa er med på å begrense hvilken del av 3D-verden som skal vises på skjermen samt å sørge for at alle verteksene omgjøres til såkalte «clip-koordinater». Disse matriseoperasjonene vil bli forklart nærmere i neste avsnitt.
I verteksshaderen er følgende parametre definert:
attribute vec3 aVertexPosition;
attribute vec4 aVertexColor;
uniform mat4 uModelViewMatrix;
uniform mat4 uProjectionMatrix;
Videre ser vi at den innebygde variabelen gl_Position settes lik aVertexPosition multiplisert med de to nevnte matrisene (NB! Må gjøres i korrekt rekkefølge, mer etter hvert).
Legg også merke til at aVertexPosition gjøres om slik at homogene koordinater benyttes. Dette gjøres vha. vec4(aVertexPosition, 1) slik at den «homogene verteksen» blir (x,y,z,1). Se eget notat om vektorer og matriser som forklarer mer om homogene koordinater.
Variabelen gl_Position er en GLSL spesifikk variabel. Hovedoppgaven til verteksshaderen er å gi denne variabelen en verdi. Som regel settes denn lik produktet av verteksen, modellview- og projeksjonsmatrisene. Verteksen sine koordinater (x,y,z,w) er nå gjort om til såkalte "clip-koordinater". Se figur under.
De ulike transformasjonene
I WebGL snakker man gjerne om følgende transformasjoner:- Modelltransformasjon
- View-transformasjonen
- De to foregående slås ofte sammen til en transformasjon (matrise): «Modelview»- transformasjonen
- Projeksjonstransformasjonen
I tillegg utføres (automatisk, vi trenger egentlig ikke tenke på dette):
- «Perspective divison», dvs. gjøre om fra homogene koordinater tilbake til kartesiske koordinater. Dette gjøres ved å dele x,y og z på den 4. koordinatverdien, w.
- Viewport-transformasjon.
Verteksshaderen
Normalt utføres både modelview-transformasjonen og projeksjonstransformasjonen i verteksshaderen vha. matrisemultiplikasjon. Dette ser vi også i kodeeksemplet over.Både viewport-transformasjonen og «perspective division» utføres (automatisk) i steget etter verteksshaderen, dvs. i steget "Sammenstilling av primitiver".
Vi ser dette i figuren under, som er et utsnitt av tidligere vist graphics pipeline.
 |
| Utsnitt av graphics pipeline |
Etter at verteksen er multiplisert med modelview-matrisa sier vi at verteksene er transformert til «øye-koordinater». Hvorfor det kalles «øye-koordinater» vil bli tydeligere når vi ser mer på view-transformasjon.
Den transformerte verteksen multipliseres så med projeksjonsmatrisa og er da transformert til «clip-koordinater». Den transformerte verteksen tilordnes til slutt i verteksshaderen til gl_Position.
Sammenstilling av primitiver (trekanter)
I neste steg av pipelinen, «Sammenstilling av primitiver», vil koordinatene som er tilordnet gl_Position, som fortsatt består av homogene koordinater, divideres med w.Verteksen er nå omgjort til såkalte NDC (Normalized Device Coordinates). Det vil si at alle vertekser som har koordinatverdier (x, y og z) i området [-1, 1] vil være med videre i pipelinen. Vertekser med koordinater utenfor dette området vil «clippes» vekk – de er ikke med videre. Primitiver som er delvis innenfor deles i to. Tenk på dette som om frustumet strekker seg fra -1 til +1 i x,y og z-retning.
Deretter utføres «viewport»-transformasjonen (dette gjøres ikke ved hjelp av en matrise), dvs. at NDC mappes til det området på skjermen som skal vise resultatet.
Beregning av dybde; z-buffer
Basert på z-verdien til NDC beregnes det en z-/dybdeverdi, i området 0-1, per fragment. Verdien legges i z-/dybde-bufret og er med på å bestemme om nye fragmenter skal vises eller ikke.Se også (OpenGL Wiki, Vertex Transformation, 2012) og her for mer info.
Rasterisering
Etter «viewport»-transformasjonen utføres rasterisering som betyr å fylle primitivene (trekantene) med nødvendige fragmenter/piksler.Modellen(e) (trekanten(e)) er nå brutt ned til et sett fragmenter. Et fragment er en «kandidat» til å bli en piksel i skjermbufret, ikke alle fragmenter ender opp som piksler i skjermbufret. Hvert fragment sendes nå til fragmenthaderen (kalles pikselshader i Direct3D-terminologi).
Fragmentshaderen
Dette er, som verteksshaderen, et program som kjøres av GPUen. Her settes eller beregnes fargen til hver enkelt piksel som utgjør det indre av trekanten.Fragmentshaderen vil typisk motta en farge som et parameter. I sin enkleste for vil fragmentshaderen kun videresende denne ved å sette gl_FragColor lik parameterverdien. Alternativt kan den f.eks. gjøre ulike lysberegninger som påvirker endelig farge på fragmentet. Uansett må fragmentshaderen sette gl_FragColor lik en verdi.
I kodeeksemplet over får alle pikslene samme farge via fragmentshader-parametret u_FragColor. Dette er også en «uniform» og har samme verdi for alle piksler. Verdien til denne sendes fra bindShaderParameters() metoden i WebGL/Javascrips-koden.
Alternativ kunne man knyttet en farge til hver verteks og brukt disse til å gi farge til pikslene til trekanten. Fargen knyttet til verteksene ville i så fall bli «interpolert» (utjevnet) over trekantenes flater.
Fragmentene går via flere steg før de ender opp i skjermbufret (framebuffer). Mer om dette senere.
Oppsummering så lang
Hele prosessen kan forenklet illustreres slik: |
| Forenklet graphics pipeline |
Transformasjonene som utføres av verteksshaderen
La oss nå se mer detaljert på de ulike transformasjonene som verteksshaderen utfører.Modelltransformasjonen
Når man opererer med mange modeller er det enklere å definere hver enkelt 3D modell i forhold til et lokalt koordinatsystem (model space) i stedet for et globalt/scene koordinatsystem. Tenk deg at du skal arrangere en miniatyrscene for et filmopptak hvor det inngår modeller som biler, hus, tog, trær osv. Modellene som skal fotograferes må bygges. I stedet for å bygge disse direkte i miniatyrverdenen vil man typisk bygge disse i et verksted (e.l.) før man plasserer dem i scenen.På tilsvarende måte konstrueres 3D modeller i WebGL. Modellene defineres i forhold til et tenkt lokalt koordinatsystem (model space) og gjerne sentrert rundt origo. Deretter "plasseres modellen" i det "globale" koordinatsystemet (world space) ved hjelp av en koordinattransformasjon / matrisemultiplikasjon. Se (Luna, 2006), (Angel E. & David S., 2015) og (Matsuda et.al, 2013, vedlegg G).
Når vi i Javascript-koden spesifiserer en modell, f.eks. en kube, oppgir vi verteksene i et tenkt lokalt koordinatsystem. Verteksene sine koordinater kalles da modellkoordinater (se tidligere figur). Vha. en modelltransformasjon kan vi posisjonere og orientere kuben i det globale koordinatsystemet (world space).
Hver enkelt modell kan har sin egen modelltransformasjon. Når alle modellene er transformert inn i det globale koordinatsystemet er alle i samme koordinatsystem. En modelltransformasjon består normalt av en eller flere av følgende i kombinasjon:
- Translasjon (forflytning)
- Rotasjon
- Skalering
Dersom man f.eks. definerer et hus spesifiserer man alle verteksene i modellkoordinater for deretter å gjøre nødvendige transformasjoner. Dette kan f.eks. bety å skalere huset opp eller ned, rotere og evt. flytte det dit man måtte ønske i forhold til det globale systemet. Se figuren under.
 |
| Modelltransformasjonen: translasjon og skalering |
Legg merke til at dersom man setter modellmatrisa lik identitetsmatrisa vil modellen «plasseres direkte» i det globale systemet.
 |
| Modellmatrisa = Identitetsmatrisa, dvs. ingen transformasjon. |
View-transformasjonen
| Plassering av «virtuelt» kamera |
Vha. view-transformasjonen kan vi posisjonere og orientere dette «virtuelle» kameraet der vi måtte ønske. I utgangspunktet, dvs. dersom view-matrisa = identitetsmatrisa, står kameraet i origo og ser langs negativ z-akse. Dette betyr at kameraet i utgangspunktet ikke nødvendigvis vil se alle modeller/figurer. For at kameraet skal se modeller som er bak eller ved siden av kameraet må enten modellene flyttes foran kameraet eller så må kameraet flyttes og roteres slik at det ser modellene.
Ved hjelp av view-matrisa transformeres verteksene til modellen(e) motsatt i forhold til hvor du ønsker å flytte kamera (man kan tenke seg at kameraet står i origo og at modellene flyttes i forhold til dette).
Dersom man tenker seg at kameraet skal flyttes +5 enheter langs z-aksen vil det vær det samme som om vi flyttet modellen(e) -5 enheter langs z-aksen. Modell- og view-transformasjonene er egentlig to sider av samme sak. Dette vil bli nærmere forklart i avsnittet om modelview-transformasjonen.
View-transformasjonen består egentlig av en kombinasjon av en translasjon og en rotasjon.
Etter view-transformasjonen er koordinatene transformert til øyekoordinater (og modellen er i «view space»).
Ved hjelp av funksjonen mat4.lookAt(parametre) kan man generere en View-matrise. Parametrene til denne funksjonen omfatter bl.a. kameraets posisjon og punktet det peker/ser mot.
Bruk av glMatrix-biblioteket (bruker også vec3-klassen):
let v3Eye = vec3.fromValues(7.0, 6.0, 16.0); //Eksempler
let v3Look = vec3.fromValues(0.0, 0.0, 0.0);
let v3Up = vec3.fromValues(0.0, 1.0, 0.0);
let viewMatrix = mat4.create();
mat4.lookAt(viewMatrix, v3Eye, v3Look , v3Up);
Bruk av cuon-matrix.js (Matsuda et.al, 2013) biblioteket:
let viewMatrix = new Matrix4();
viewMatrix.setLookAt(eyeX, eyeY, eyeZ, lookX, lookY, lookZ,
upX, upY, upZ);
Eye-koordinatene tilsvarer kameraets posisjon. Look- koordinatene tilsvarer punktet kameraet peker mot og Up- koordinatene definerer hva som er opp/ned på kameraet (som regel upX=0, upY=1, upZ=0).
Når man spesifiserer viewmatrisa er det selvfølgelig viktig at kameraet peker mot modellen(e), hvis ikke vil den ikke vises på skjermen. Som vi straks skal se vil også projeksjonsmatrisa være med på avgrense hva som ender opp på skjermen.
Modelview-transformasjonen
Modell- og viewtransformasjonene er i praksis to like operasjoner i forhold til hvordan den endelige scenen blir seende ut. Det viktige er forholdet mellom kameraet og modellen(e) i scenen. Anta at et kamera og en modell som begge er plassert i origo og at kameraet ser mot negativ z-akse. Dersom kameraet skal «se» modellen må enten modellen flyttes mot negativ z eller kameraet mot positiv z. Begge operasjonene er i prinsippet samme ting.Enten flytter man modellen i den ene retninga eller så flytter man kameraet i motsatt retning.
Begrepet «modelview» betyr at modell- og viewtransformasjonsmatrisene slås sammen til en matrise.
I enkelte tilfeller kan det være praktisk å håndtere disse som to separate matriser men de må uansett slås sammen for å få utført korrekt transformasjoner på verteksene. I praksis vil man ofte slå sammen disse to matrisene i Javascript-koden og sende resultatmatrisa (altså «modelview-matrisa») til verteksshaderen. Alternativt kan begge sendes inn til shaderen som da får ansvaret for å multiplisere disse sammen.
I tidligere versjoner av både standard OpenGL og ES-versjonen var det ikke støtte for programmerbare shadere («fixed function pipeline») og her opererte man kun med modelview-matrisa.
Projeksjonstransformasjonen
Denne transformasjonen skjer etter modelview-transformasjonen. Transformasjonen sørger for å projisere den delen av 3D-verdene/scenen som kameraet peker mot til en 2D-flate (skjermen). Den bestemmer også hvordan «viewvolumet» ser ut og begrenser dette til en «enhetskube» som strekker seg fra -1 til 1 i alle tre akser (x,y,z).En vanlig analogi innen 3D grafikk er å sammenlikne modell-, view- og projeksjonstransformasjonene med det å ta et bilde med et kamera. Modelltransformasjonen tilsvarer det å plassere modellene i scenen. View-transformasjonen tilsvarer å plassere og orientere kameraet mot modellene(e) mens projeksjonstransformasjonen tilsvarer det å velge en linse til kameraet. Kameralinsa påvirker hva kameraet ser og til en viss grad hvordan modellene vil se ut.
Det finnes to typer projeksjoner:
- Ortografisk projeksjon
- Perspektivprojeksjon
Ortografisk projeksjon
Ortografisk projeksjon kalles også parallell projeksjon siden parallelle linjer fortsatt er parallelle etter projeksjonen. Ortografisk projeksjon betyr også at størrelsen til modeller ikke påvirkes av avstanden til kameraet - man får dermed ingen dybdefølelse. Man får med andre ord mindre realisme i scenen som fremvises. 3D effekten blir mindre om ikke fraværende. Ortografisk projeksjon kan imidlertid være nyttig i CAD (Computer Aided Design) - systemer eller om man ønsker å lage 2D grafikk i WebGL.Når ortografisk projeksjon brukes vil «view-volumet» være en rektangulær boks. Primitiver (trekanter) som faller innenfor volumet vil projiseres på «near-plane» (se figur under) og vises i den endelige scenen. Primitiver som er delvis innenfor vil «klippes»/deles opp. Resten vil ikke vises, dvs. verteksene til primitiver som faller utenfor blir ikke sendt videre i «pipelinen».
Man kan f.eks. bruke mat4.ortho(…) funksjonen, definert i glMatrix, til å generere en ortografisk matrise:
- mat4.ortho(left, right, bottom, top, near, far, projectionMatrix);
Perspektivprojeksjon
Når man bruker perspektivprojeksjon vil modeller som er langt unna kamera virke mindre enn de som er nærmere kamera. Dette gir en mer realistisk fremstilling og dermed en bedre 3D illusjon siden det er slik våre øyne fungerer – ting som er langt unn virker mindre enn det som er rett ved siden av oss.View-volumet som genereres ved perspektivprojeksjon kalles et frustum som ser ut som en avkappet pyramide.
| View frustum |
Vertekser (og dermed primitiver og objekter) som ligger helt eller delvis innenfor denne pyramiden representerer det som kameraet ser. Denne transformasjonen sørger dermed for to ting:
- hvordan objekter projiseres til 2D (skjermen)
- hvilke objekter eller deler av objekter som skal utelates i det endelige bildet
Det er to typer funksjoner man kan bruke til å generere en projeksjonsmatrise:
- perspective() / setPerspective()
- frustum()
glMatrix-biblioteket:
let projectionMatrix = mat4.create();
mat4.perspective(fovy, aspect, near, far, projectionMatrix);
cuon-matrix.js:
let projectionMatrix = new Matrix4();
projectionMatrix.setPerspective(fovy, aspect, near, far);
Parametrene er som følger:
- fovy: vertikal “field of view” (i grader, f.eks. 45)
- aspect: bredde til viewport / høyde til viewport (eks. canvas.width / canvas.height)
- near: near clipplane (f.eks. 1)
- far: fra clipplane (f.eks. 1000)
- projectionMatrix: resultatmatrisa etter kall på denne funksjonen
| Perspektivmatrise beregnet vha. setPerspective() (Matsuda et.al., 2013) |
Man kan også bruke frustum() funksjonen til å generere en perspektivmatrise. Denne har parametrene (glMatrix):
Matrisa kan beregnes slik:
Vi har nå en projeksjonsmatrise. Denne sendes inn til verteksshaderen, på samme måte som modelviewmatrisa. Se kodeeksemplet over.
Perspektivprojeksjon består egentlig av en kombinasjon av skalering og translasjon.
Figuren viser alle transformasjoner som utføres fra modellen spesifiseres vha. modellkoordinater til modellen ender opp på skjermen i skjermkoordinater. Modellkooridinatene multipliseres med modellmatrisa slik at de transformeres til "world" koordinater. Disse multipliseres med view-matrisa og gir "øye"-koordinater (NB! som regel utføres dette i et steg ved at modellkoordinatene multipliseres med modelview-matrisa). Disse multipliseres med projeksjonsmatrisa og verteksene er i "clip"-koordinater som også er det som verteksshaderen leverer fra seg. Resten håndteres av "pipelinen": Neste steg er å konvertere fra homogene koordinater (verteksshaderen opererer med homogene koordinater) til kartesiske koordinater ved å dele på w. Vi har nå normaliserte koordinater (NDC). Disse gjøres til slutt om til skjermkoordinater vha. "viewport"-transformasjonen.
Se Vedlegg1 for komplett gjennomgang og talleksempel.
- mat4.frustum(left, right, bottom, top, near, far, projectionMatrix);
Matrisa kan beregnes slik:
| Perspektivmatrise beregnet vha. frustum() (Sellers et.al., 2014) |
Perspektivprojeksjon består egentlig av en kombinasjon av skalering og translasjon.
Oppsummert
Hele prosessen kan oppsummeres i følgende figur:Se Vedlegg1 for komplett gjennomgang og talleksempel.
Mer om clipping & culling
Vertekser og trekanter som faller innafor frustumet vil kunne ende opp på skjermen. En trekant kan ha tre posisjoner i forhold til frustumet:- Innenfor
- Utenfor
- Delvis innenfor
Det kan nevnes at moderne grafikkort automatisk ”culler” det som faller utenfor frustumet. Men, og dette er viktig, det betyr ikke at WebGL-programmet automatisk vet hvilke objekter som ligger innafor frustumet og hvilke som ligger utenfor (dette bestemmes jo av View og projeksjonsmatrisene). Dette betyr igjen at dersom vi har en stor scene med mange objekter som skal tegnes og kameraet peker en vei vil tegnekommandoen (drawArrays()) bli utført for alle objekter uansett om de ligger innafor eller utenfor frustumet. Grafikkortet/pipelinen vil imidlertid sørge for å fjerne objekter som faller utenfor.
For mer effektiv tegning/rendring kan man allerede i WebGL-koden sørge for at det som faller utenfor frustumet ikke tegnes – dette kalles frustum culling. For enda bedre resultat kan man også sørge for ikke å tegne objekter som ligger bak andre objekter og som uansett ikke skal vises – kalles occlusion culling.
Oppsummering av kodeeksemplet
I kodeeksemplet over var det vist hvordan modelview og projeksjonsmatrisene sendes til, og brukes av, verteksshaderen for å transformere hver verteks til modellen(e). Legg merke til at modellmatrisa inneholder en «translasjon»/forflytning, -30 på x-aksen. Dette betyr at modellen (trekanten) flyttes litt til venstre før den plasseres i det globale koordinatsystemet og på skjermen. Modellmatrisa kan enkelt endres slik at den også inneholder en rotasjon og/eller en skalering. Prøv f.eks. å endre koden i draw() slik:. . .
// Definerer modellmatrisa (rotasjon + translasjon):
modelMatrix.setTranslate(-20, 10, 0);
modelMatrix.rotate(45, 0, 0, 1);
. . .
Dette gjør at modellen først roterer 45 grader om egen akse for deretter å flytte -30 langs x-aksen. Her settes, vha. setTranslate(), modellmatrisa først lik en translasonsmatrise. Denne multipliseres så med en rotasjonsmatrisa ved hjelp av rotate() metoden. Metoder som starter med set, f.eks. setTranslate(), nullstiller og oppretter en ny matrise som kun inneholder en translasjon. Metoder uten set, som rotate(), endrer (her) modelMatrix ved å multiplisere med en rotasjonsmatrise.
Siste del av graphics pipeline
Her omtales kort de siste blokkene i figuren (over) som viser OpenGL ES graphics pipeline.Scissor test, Stencil test, Depth test, Blending
Den nest siste blokka kalles «Diverse fragment/piksel-operasjoner». Disse omtales kort her.Selv om pikselfargene er beregnet og returnert fra fragmentshaderen kan fragmentet fortsatt bli forkastet pga. ulike tester som utføres i dette steget.
Scissor test:
Man kan sette et såkalt ScissorRectangle for å begrense tegning til en mindre del av skjermen/vinduet. Settes på GraphicsDevice-objektet.
Stencil test:
Bruker et spesielt buffer, et stencil buffer, og brukes i spesielle tilfeller til avanserte rendringteknikker.
Depth test:
Ved hjelp av verteksene beregnes også dybdeinformasjon til hver enkelt fragment – hver enkelt fragment har tilknyttet dybdeinformasjon. Dette lagres i et eget buffer som kalles z-buffer eller bare dybde(depth) buffer. Dette er med på å avgjøre hvilke modeller som ligger fremst i bildet og dermed skal vises og hvilke som ikke skal med i det endelige bildet.
Alpha blending:
Dersom alpha blending benyttes vil fragmentets farge blandes med fargen til andre fragmenter (som ligger over eller under).
Frame buffer
I det siste steget i pipelinen lagres pikslene i frame bufret som også er det som til slutt vises på skjermen.Eksempel: Fra modellkoordinater til skjermkoordinater
Se gjennomgang i Vedlegg 1 (ikke pensum). Viser alle transformasjonenene, med tallverdier, fra verteksene sendes inn til verteksshaderen til trekanten ender opp på skjermen.Tegne en kube
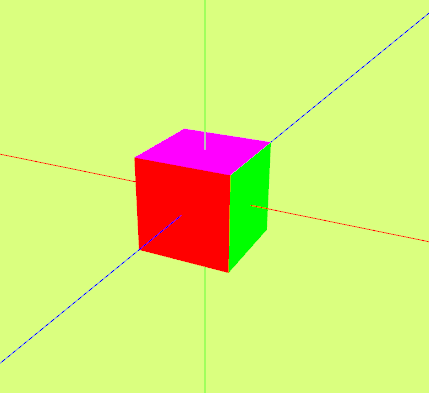
I dette avsnittet skal vi se hvordan man kan definere og tegne en kube som tegnes i perspektiv ved hjelp av view- og projeksjonsmatrisene. Sidene til kuben skal ha ulike farger og skal se omtrent slik ut.Vi tar utgangspunkt i følgende figur for å definere nødvendige vertekser:
Her ser vi kuben og verteksposisjonene til kubens hjørner. Det er også antydet at hver siden av kuben består av to trekanter. I tillegg er koordinataksene vist. Dersom kuben tegnes vha. drawArrays(gl.TRIANGLES, …) kan følgende verteksposisjonsarray benyttes:
//KUBEN:
//36 stk posisjoner:
let cubeVertices = new Float32Array([
//Forsiden (pos):
-1, 1, 1,
-1,-1, 1,
1,-1, 1,
-1,1,1,
1, -1, 1,
1,1,1,
//Høyre side:
1,1,1,
1,-1,1,
1,-1,-1,
1,1,1,
1,-1,-1,
1,1,-1,
//Baksiden (pos):
1,-1,-1,
-1,-1,-1,
1, 1,-1,
-1,-1,-1,
-1,1,-1,
1,1,-1,
//Venstre side:
-1,-1,-1,
-1,1,1,
-1,1,-1,
-1,-1,1,
-1,1,1,
-1,-1,-1,
//Topp:
-1,1,1,
1,1,1,
-1,1,-1,
-1,1,-1,
1,1,1,
1,1,-1,
//Bunn:
-1,-1,-1,
-1,-1,1,
1,-1,1,
-1,-1,-1,
1,-1,1,
1,-1,-1
]);
For å få farge på kubens side angir vi også en farge per verteks vha. følgende array:
//Ulike farge for hver side:
let colors = new Float32Array([
//Forsiden:
1.0, 0.0, 0.0, 1,
1.0, 0.0, 0.0, 1,
1.0, 0.0, 0.0, 1,
1.0, 0.0, 0.0, 1,
1.0, 0.0, 0.0, 1,
1.0, 0.0, 0.0, 1,
//Høyre side:
0.0, 1.0, 0.0, 1,
0.0, 1.0, 0.0, 1,
0.0, 1.0, 0.0, 1,
0.0, 1.0, 0.0, 1,
0.0, 1.0, 0.0, 1,
0.0, 1.0, 0.0, 1,
//Baksiden:
1.0, 1.0, 0.0, 1,
1.0, 1.0, 0.0, 1,
1.0, 1.0, 0.0, 1,
1.0, 1.0, 0.0, 1,
1.0, 1.0, 0.0, 1,
1.0, 1.0, 0.0, 1,
//Venstre side:
0.0, 0.0, 1.0, 1,
0.0, 0.0, 1.0, 1,
0.0, 0.0, 1.0, 1,
0.0, 0.0, 1.0, 1,
0.0, 0.0, 1.0, 1,
0.0, 0.0, 1.0, 1,
//Topp
1.0, 0.0, 1.0, 1,
1.0, 0.0, 1.0, 1,
1.0, 0.0, 1.0, 1,
1.0, 0.0, 1.0, 1,
1.0, 0.0, 1.0, 1,
1.0, 0.0, 1.0, 1,
//Bunn:
0.5, 0.7, 0.3, 1,
0.5, 0.7, 0.3, 1,
0.5, 0.7, 0.3, 1,
0.5, 0.7, 0.3, 1,
0.5, 0.7, 0.3, 1,
0.5, 0.7, 0.3, 1
]);
Oppgave:
Som vist kan man tegne en kube ved å angi 36 verteksposisjoner og farger og bruke drawArrays(gl.TRIANGLES…) til å tegne kuben. En annen mulighet er å bruke færre verteksposisjoner og drawArrays(gl.TRIANGLE_STRIP, …). Definer så få vertekser som nødvendig for å kunne tegne en kube vha. drawArrays(gl.TRIANGLE_STRIP, …)Bruker vi indekser til å tegne kuben holder det å angi 8 vertekser i tillegg til 36 indekser.
Tegn samme kube vha. indekser og drawElements(). Bruk følgende figur som utgangspunkt for å definere kubevertekser og indekser:

Kuben består av 8 vertekser der en verteks har sin posisjon, f.eks. [-1,1,1]. Verteksene gjenbrukes vha. indekser. Hver side av kuben består av to trekanter definert av 6 indeksverdier som vist i lista til høyre i figuren. Fronten av kuben er f.eks. definert av trekantene tilsvarende indeksverdiene 0,1,2 og 0,2,3. Her angis verteks(indeksene) til trekantene mot klokka.
Kuben består av 8 vertekser der en verteks har sin posisjon, f.eks. [-1,1,1]. Verteksene gjenbrukes vha. indekser. Hver side av kuben består av to trekanter definert av 6 indeksverdier som vist i lista til høyre i figuren. Fronten av kuben er f.eks. definert av trekantene tilsvarende indeksverdiene 0,1,2 og 0,2,3. Her angis verteks(indeksene) til trekantene mot klokka.


Ingen kommentarer:
Legg inn en kommentar